Exponentially weighted averages

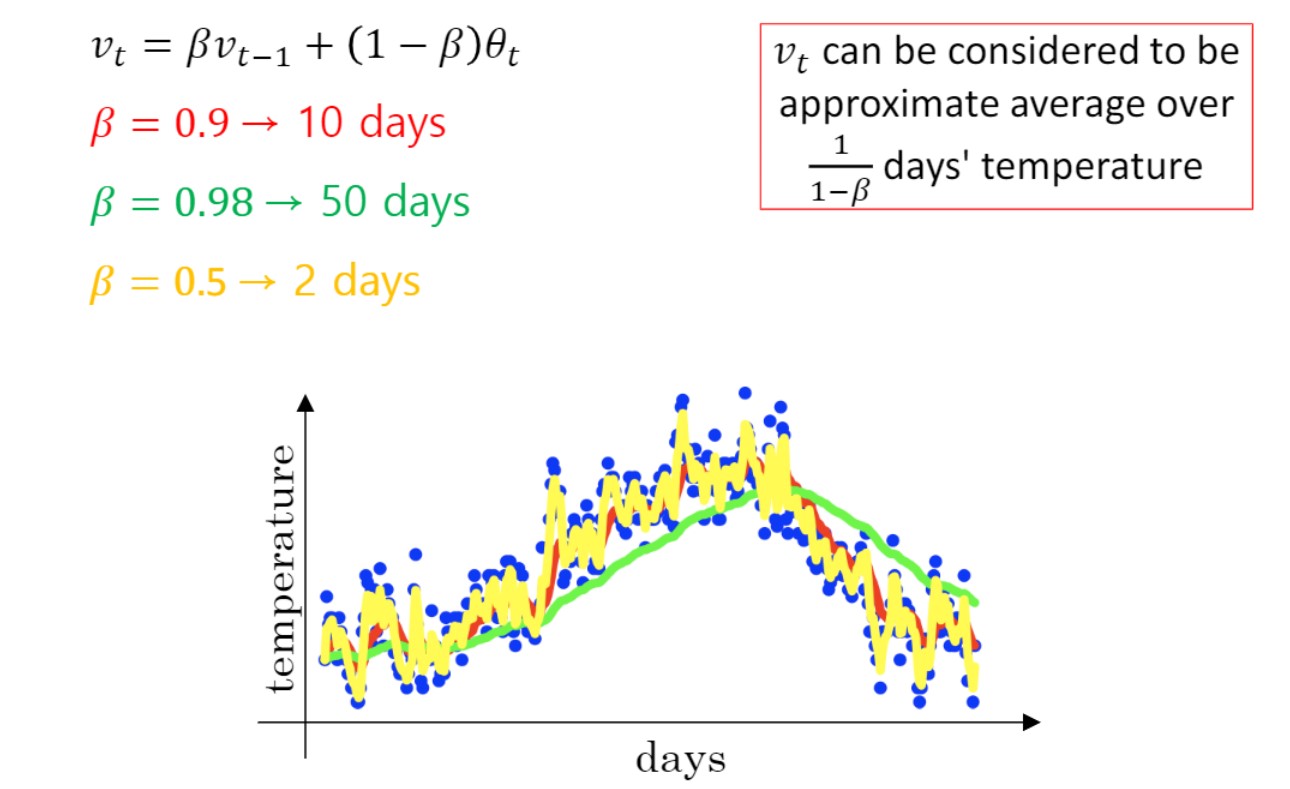
$\beta$ 값을 통해 과거 데이터에 기반해 smoothing 할 수 있다.

($\beta$ = 0.9 를 통해 과거 데이터에 더 많은 가중치. 현대 값에는 0.1의 가중치 준다.)

계산식은 위와 같음

Bias correction

Exponentially weighted averages (지수가중평균)를 이용하면 초기 구간에 오차가 있다. 앞쪽의 값이 0에 가깝다는 문제.

아래 이미지의 좌측 하단을 보면 weight의 합이 1보다 훨씬 작음.

이 문제를 해결하기 위해서는

이미지에도 나와있듯, $v_t$를 $1-\beta^t$로 나눈다.

이 경우 t가 작을때만 영향을 줌. t가 큰 경우 bias correction 거의 무시되게 된다.

이렇게 bias correction을 진행해주면, 0.0196 + 0.02였던 weight의 합이 0.49 + 0.51로 변경되어 거의 1에 가까워진 것을 볼 수 있다.

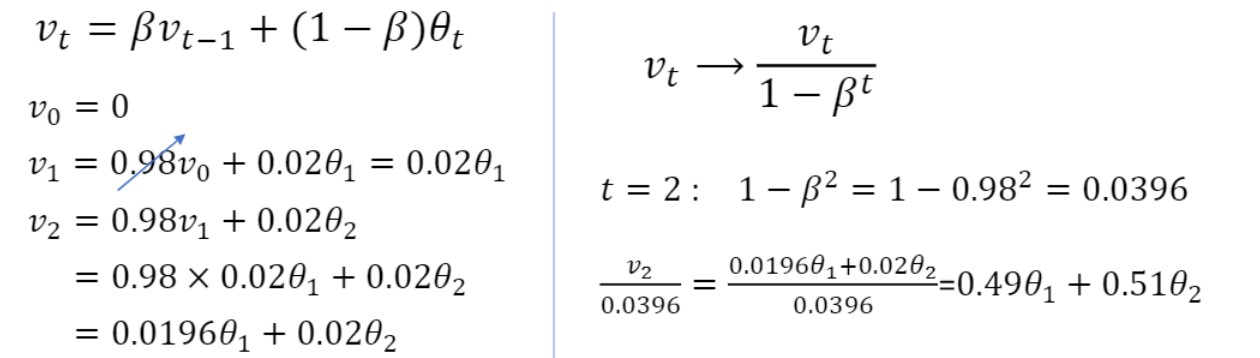
Gradient descent with momentum

Momentum은 최적의 해를 향해 진행하던 속도에 관성을 주어 1) 느린 학습속도, 2) saddle point 학습 종료, 3) 진동 심한 점 등을 해결.
-> 진행하던 속도에 관성이 적용.
$\therefore$ saddle point, local minima에서 벗어날 수 있음

Gradient의 average version

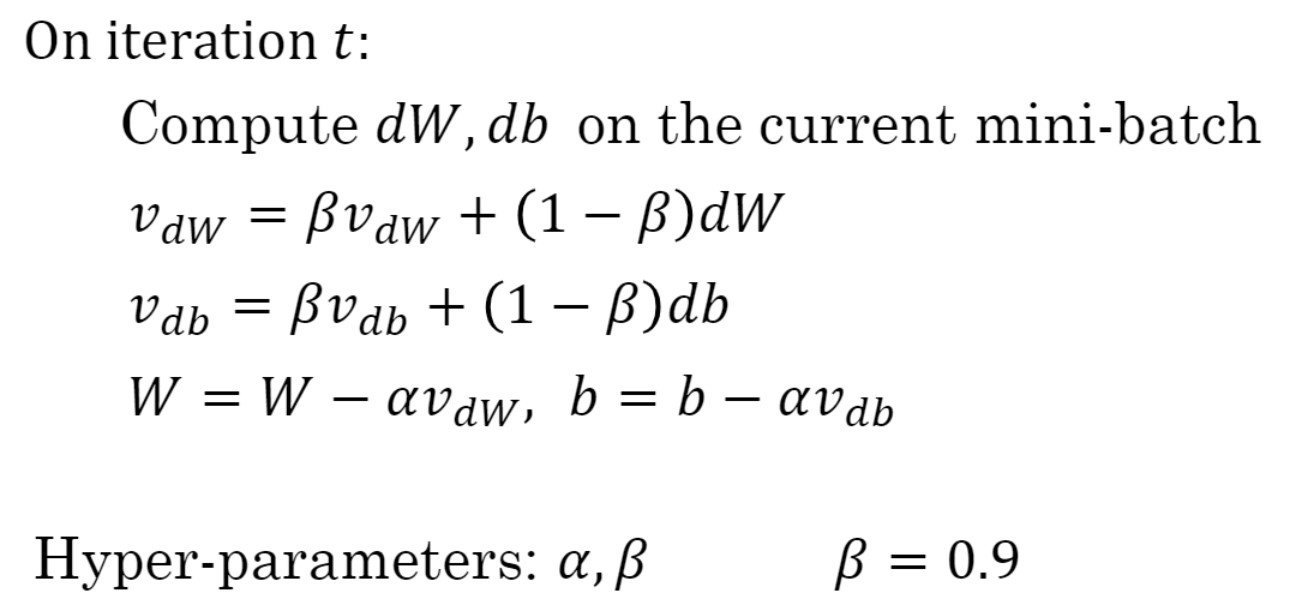
위 수식처럼 smoothed gradient가 업데이트 시 사용됨.

이때 하이퍼파라미터 $\alpha$ : controls update depth, $\beta$ : controls smoothness.
$\beta$값으로는 0.9 많이 씀.

RMSProp

: root mean square propagation

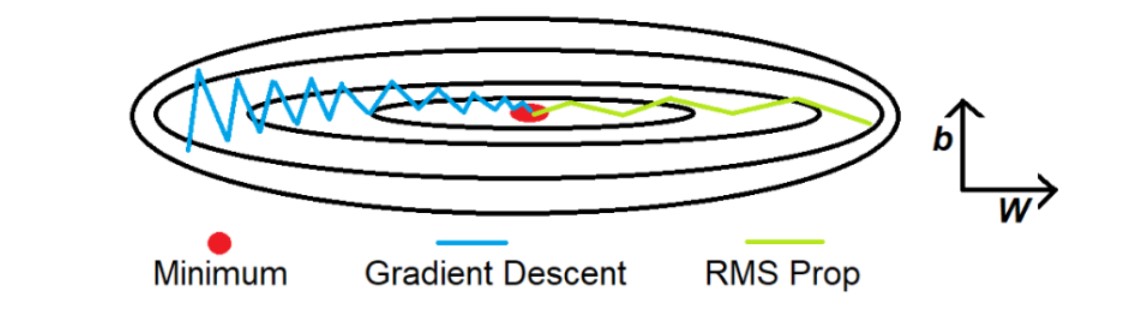
위 그림과 같이 찌그러진 경우 업데이트 할 때 수직이 아닌 수평방향으로의 이동이 중요하다. $\therefore$ 수직방향으로 탐색 $\downarrow$, 수평방향으로 더 이동.

ADAM

: 최근 많이 사용. Gradient & RMS 둘 다 사용

$v_{dW} = \beta_1 v_{dW} + (1-\beta_1)dW,$ $v_{db} = \beta_1 v_{db} + (1-\beta_1)db$
$S_{dW} = \beta_2 S_{dW} + (1-\beta_2)dW^2,$ $S_{db} = \beta_2 S_{db} + (1-\beta_2)db^2$

$v_{dW}^{corrected} = v_{dW}/(1-\beta_1^t),$ $v_{db}^{corrected} = v_{db}/(1-\beta_1^t)$
$S_{dW}^{corrected} = S_{dW}/(1-\beta_2^t),$ $S_{db}^{corrected} = S_{db}/(1-\beta_2^t)$

$W:= W-\alpha\dfrac{v_{dW}^{corrected}}{\sqrt{S_{dW}^{corrected}+\epsilon}}$
$b:= b-\alpha\dfrac{v_{db}^{corrected}}{\sqrt{S_{db}^{corrected}+\epsilon}}$

Hyperparameters choice

$\alpha$ : needs to be tuned
$\beta_1$ : 0.9(weighted average for $dW$)
$\beta_2$ : 0.999(weighted average for $dW^2$)
$\epsilon$ : $10^{-8}$

(생략)
learning rate decay
problems of plateaus

출처 : 2023-1 ITE4052 수업