Amortized Analysis

이전까지 operation의 asymptotic boundary 구했음. (e.g. sort 비교횟수-> boundary)

이 chapter에서는, push-pop 할때 push와 pop 수행시간 각각 구해서 합하는게 아닌, push, pop 합해서 n번 발생했을 때 전체 cost 구하는 것.

= 독립적으로 시간복잡도 구하는 것이 아닌, 여러 operation의 시퀀스 한꺼번에 시간복잡도 분석.

(최악의 경우를 과하게 잡지 않도록)

특정 일을 할 때 100번 진행하는 경우 99번 1분이 걸리고, 1번정도 10분이 걸린다. 이때 최악의 경우 10분으로 잡고 이 일을 반복하는 횟수를 곱하게 되면 너무 과하게 upper bound를 잡는다는 것에서 시작.
각 시퀀스의 upper bound를 구하고 이를 진행 횟수만큼 곱하는 것이 아닌 한번 진행할 때에 대한 평균적 시간을 구해서 upper bound를 구하자.
n회 진행 시 총 걸리는 시간 T(n)을 구할 수 있다면 T(n)/n이 한번 진행시 걸리는 시간이고, 이것이 한번 진행했을 때 최악의 시간(위 예시에서 10분) 보다 짧다면 평가절하를 줄인것.

amortized 예시
참고

Contents

➖ Aggregation analysis
☑️ Accounting method
➖ Potential method
➖ Dynamic Table

Accounting method

Amortized analysis의 수행시간 분석하는 두번 째 방법

어떤 연산에 대해 cost 할당할 때 나중을 위한 credit 값도 함께 할당하는 것

  • 다른 operation에 다른 charge 할당하는 것.
    몇몇 operation은 실제 cost보다 적거나 많게 charge됨.

  • credit: 자료구조의 특정 object에 변화량 할당
    이걸로 나중의 실제 cost보다 적은 amortized cost를 가지는 operation pay할 때 도울 수 있음.

3

위 이미지 설명
$\hat{c_i}$인 amortized cost가 upper bound가 되도록 설정.
실제로 각각의 operation에서는 amortized cost가 실제 cost보다 작을수도, 클수도 있음.

결국 accounting method에서 하고자 하는건,
Amortized cost = actual cost + credit
위와 같이 정의해두고, 특정 operation에 적절한 credit을 할당함으로써 (나중에 다른 operation에서 쓰임) tighter cost를 구하는 것.

정의로는 잘 와닿지 않아서 예시 확인!

예시1: Stack operation

  • 각 operation의 actual cost
    • PUSH : 1
    • POP : 1
    • MULTIPOP(k) : $min(k,s)$
      k: parameter, s: current stack data #
  • 각 operation의 amortized cost
    • PUSH : 2
      actual cost 1 + credit 1
    • POP : 0
    • MULTIPOP(k) : 0

아래와 같이 빈 stack에서 시작을 한다면,
4

PUSH operation을 1회 진행 한 경우 5

actual cost 1 + (나중을 위한) credit 1
$\therefore$ Amortized cost
= actual cost + credit = 2

PUSH 2회 더 진행한 결과 6

POP operation 1회 진행 7

POP과 MULTIPOP은 credit 1씩 사용

이 때 amortized cost는,
actual cost - credit = 0

여기에 다시 PUSH 진행 8

Amortized cost : actual cost 1 + credit 1 = 2

  • POP과 MULTIPOP은 반드시 PUSH operation 이후에 실행되어야 함.
    $\therefore$ PUSH에 조금 더 charge (credit)
    그리고 이 credit으로 POP과 MULTIPOP이 cost를 pay

  • credit의 양은 음수일 수 없음(nonnegative)
    stack은 항상 nonnegative object가지고 있기 때문.
    $\therefore$ total amortized cost는 total actual cost의 upper bound

  • Total amortized cost : $O(n)$

          (total actual $\le$ total amortized)

  • Total actual cost : $O(n)$

예시2: Binary counter

  • actual cost
    • Bit set (0 -> 1) : 1
    • Bit reset (1 -> 0) : 1
  • amortized cost
    • Bit set : 2
    • Bit reset : 0

Bit set 1회 9

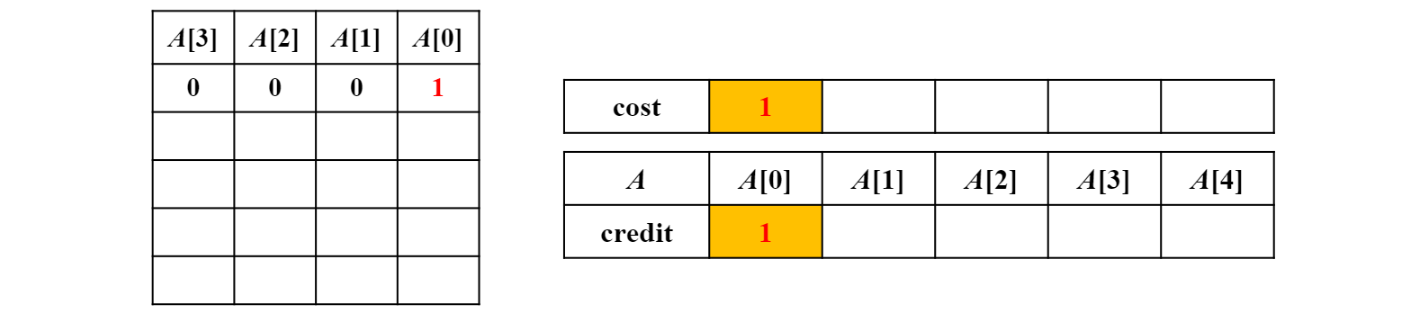
Amortized cost : actual 1 + credit 1 = 2

Bit reset 1회 10

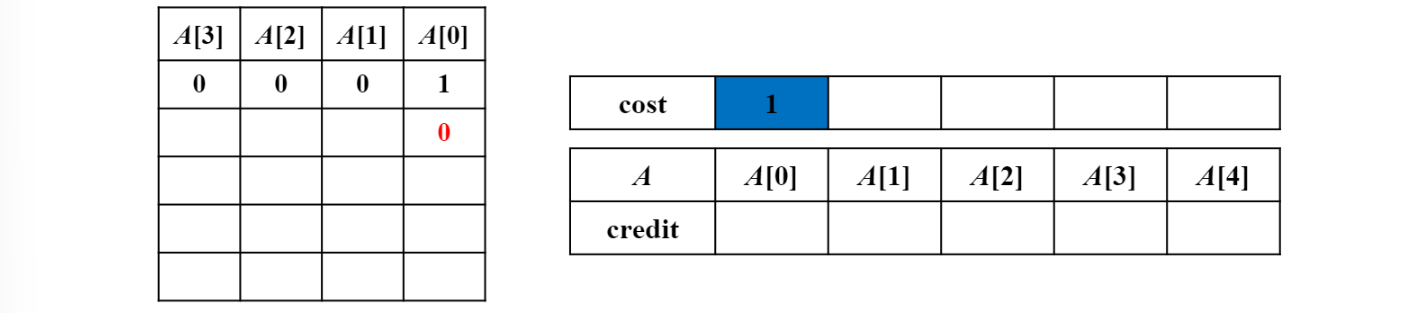
Amortized cost : actual 1 - credit 1 = 0

Bit set 1회 11

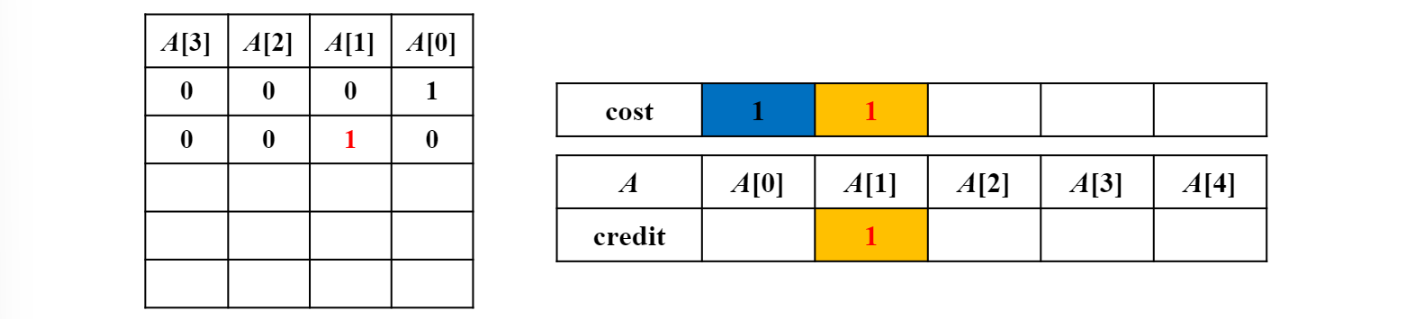
Amortized cost : actual 1 + credit 1 = 2

(0011을 만들기 위해 Bit set 1회)
(0100을 만들기 위해 Bit reset 2회, Bit set 1회) 위 두가지 했을 때의 상태 ![12][12]

  • 각 Bit reset은 각 Bit set 이후에 실행(execute)되어야함
    $\therefore$ Bit set에 조금 더 charge (credit)
    그리고 이 credit으로 Bit reset이 cost를 pay

  • credit의 양은 음수일 수 없음(nonnegative)
    $\because$ counter의 1은 음수가 될 수 없기 때문.
    $\therefore$ total amortized cost는 total actual cost의 upper bound ⭐

  • Total amortized cost : $O(n)$

  • Total actual cost : $O(n)$

Amortized cost

$O(n)$ time in total

Running time

$O(n)$ time in total

✏️ 결국 Accounting method는,
POP이전에 PUSH가 와야하는것, 그리고 Bit reset 이전에 Bit set이 와야 한다는 것을 이용해
먼저 와야하는 것에 cost를 더 할당하고 뒤에 오는것에는 그만큼 cost를 덜 할당하는 방법으로 tighter bound를 구한다.
이 때 cost의 차이는 credit을 통해 추가하고 빼는 방식 사용.

= credit 사용한 가상의 수행시간을 설정함. 그리고 이때 가상의 수행시간은 actual 수행시간보다 길어야함!
가상의 수행시간의 합을 upper bound로 설정.

출처 : 2023-2 ITE2039 수업