Dynamic Programming_Rod cutting (2/4)

Dynamic Programming

: 알고리즘의 한 종류.
(메모리를 좀 더 쓰고 대신 시간 절약하는 방법중 하나)
계산 결과를 저장해 두었다가 추후에 다시 사용.
DP라는 이름과의 연관성 낮음

큰 문제를 작은 문제로 나눠 푸는 것.
divide conquer와 비슷. 다만 작은 문제의 중복 유무가 큰 차이
dynamic programming은 작은 문제들이 반복 O

Contents
➖ Assembly-line scheduling
☑️ Rod cutting
➖ Longest common subsequence
➖ Matrix-chain multiplication

Rod cutting

막대기 갈라서 파는 경우.
n의 길이의 rod와 $i$의 길이 별 가격 table $p_i$가 있을 때 rod 잘라 벌 수 있는 최대 수익 $r_n$ 구하기
(= 길이 n인 경우 돈 가장 많이 벌기 위해 어떻게?)

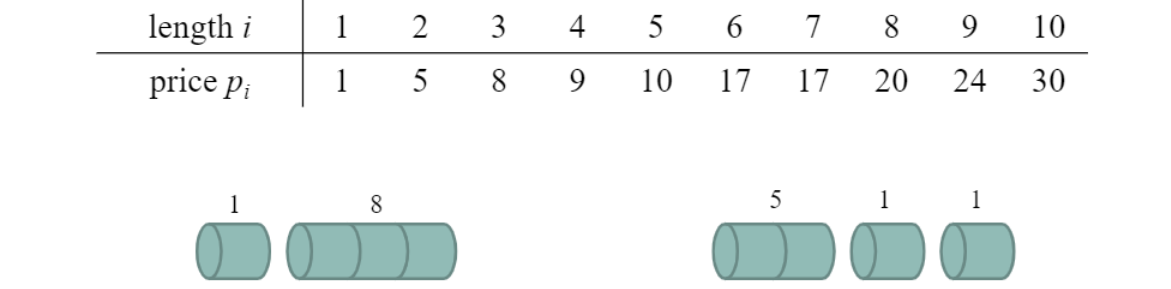
naive한 방법

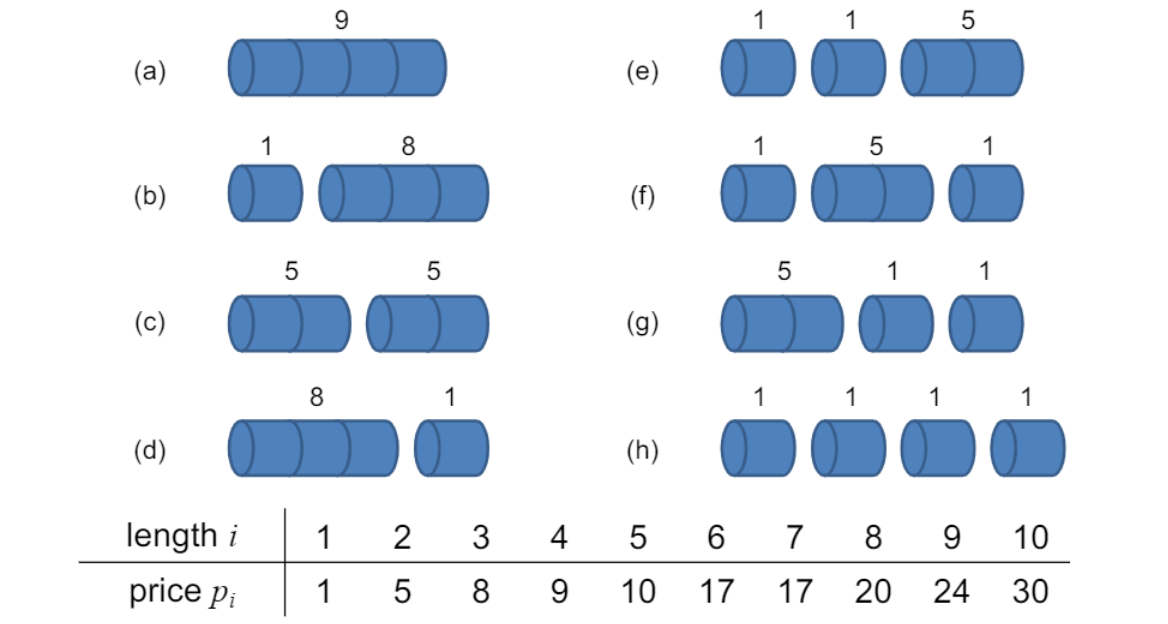
모든 가능한 방법을 계산(가능한 모든 경우의 수 탐색) 후 가장 빠른 길을 찾음
단순히 $2^3$ 아님 ($\because$ e,f,g는 동일)

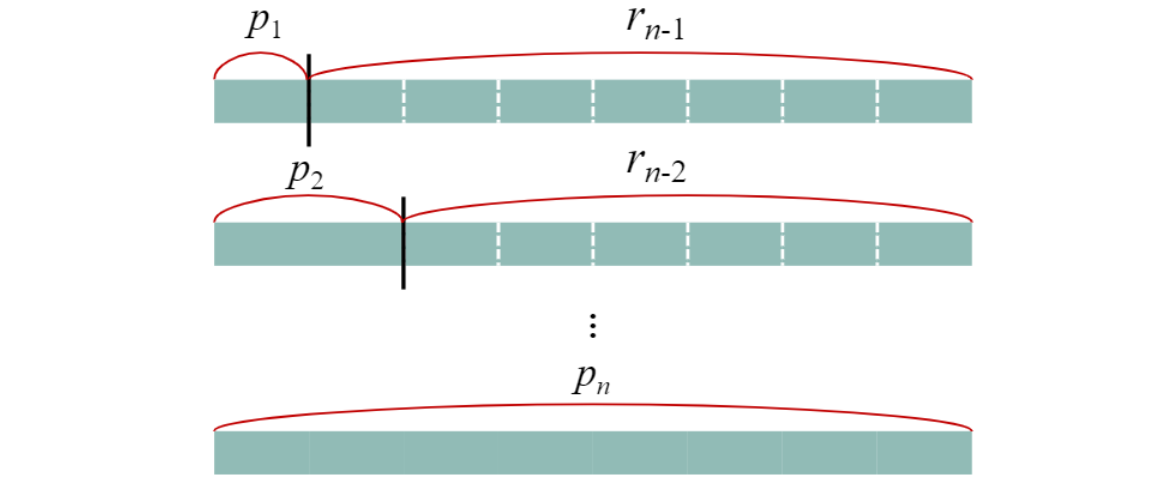
=> $r_n=max_{1\leq i\leq n}(p_i+r_{n-i})$

DP 핵심:
풀고자 하는 문제 recurrence로 정의 가능한가?
위의 수식도 recurrence로 풀되, 작은 것 찾아갈 때 값 기억해 두는 것.

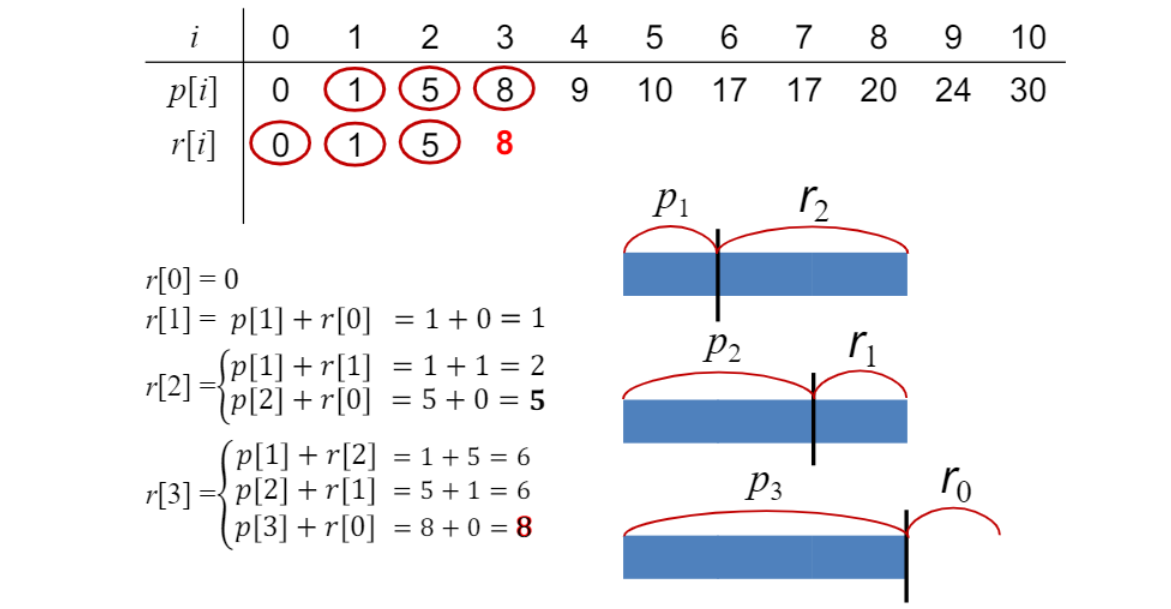
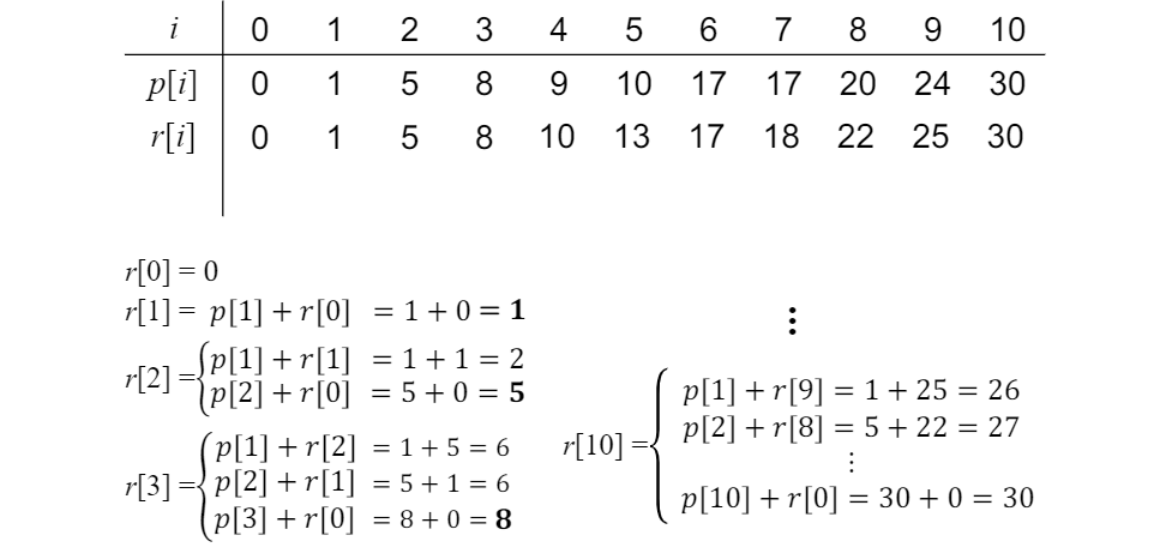
$r[i]$가 assembly line의 table $s$

$i$가 9인 경우, 가능한 p[j] + r[i-j]경우는,

p[1] + r[8]
p[2] + r[7]
p[3] + r[6]
...
p[9] + r[0]

이 중 p[3]+r[6]이 최대.
또한 r[6]은 또 분할 될 수 O(p아닌 r이어서)
-> 매번 구하기 귀찮다면 기록해 두면 됨

최대가 되는 값 어떤것 선택한건지는 하나씩 비교해 보면 알 수 O

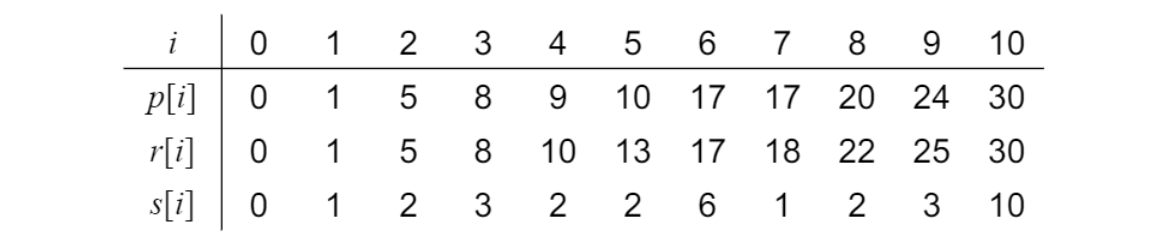
$s[i]$는 어딜 잘라서 최대 revinue 얻었는지 표기

$i$가 5인 경우, p[2]+r[3]
- - | - - -
-> 자르는 위치는 2

$i$가 9인 경우, p[3]+r[6]
- - - | - - - - - -
-> 자르는 위치는 3
(다시 r[6] 가야함)

pseudo code

EXTENDED-BOTTOM-UP-CUT-ROD(p,n)
    let r[0..n] and s[0..n] be new arrays
    r[0] = 0
    for j = 1 to n
        q = -∞ # 지금까지 중 최댓값 기록하는 변수
        for i = 1 to j
            if q < p[i] + r[j-i]
                q = p[i] + r[j-i] # q보다 크면 update
                s[j] = i # update 시 i값 s에 기록해두기
        r[j] = q # 최댓값인 q를 r에 기록
    return r and s

=> $ \theta(n^2)$

PRINT-CUT-ROD-SOLUTION(p,n) # 길이가 9인 경우,
    (r,s) = EXTENDED-BOTTOM-UP-CUT-ROD(p,n)
    while n > 0
        print s[n] # 3 출력,
        n = n -s[n] # n=6으로 다시(r[6])

=> $ O(n)$ : 최악의 경우 1개 씩. 최대 n번

Space consumption

$\theta(n)$

Running time

$\theta(n^2)$
1+2+3+4+ … +n = n(n+1)/2

DP에서 시간복잡도 구할 때,(위 pseudo code 참고)
r[i]한 칸 채우는데 얼마나 걸리는지 보면 됨
j를 채울 때 (1,j-1), (2,j-2), … j 개의 pair를 봐야 함
$\sum_jj$ $\therefore n^2$에 비례

assembly-line scheduling 처럼 table r을 table s로 줄일 수 있나?

	Space	Time
Assembly-line scheduling	$\theta(n)$	$\theta(n)$
Rod cutting	$\theta(n)$	$\theta(n^2)$
Longest common subsequence
Matrix-chain multiplication

출처 : 2023-2 ITE2039 수업