Dynamic Programming

: 알고리즘의 한 종류.
(메모리를 좀 더 쓰고 대신 시간 절약하는 방법중 하나)
계산 결과를 저장해 두었다가 추후에 다시 사용.
DP라는 이름과의 연관성 낮음

큰 문제를 작은 문제로 나눠 푸는 것.
divide conquer와 비슷. 다만 작은 문제의 중복 유무가 큰 차이
dynamic programming은 작은 문제들이 반복 O

Contents
☑️ Assembly-line scheduling
➖ Rod cutting
➖ Longest common subsequence
➖ Matrix-chain multiplication

Assembly-line scheduling

(제조현장에서) 조립 공정

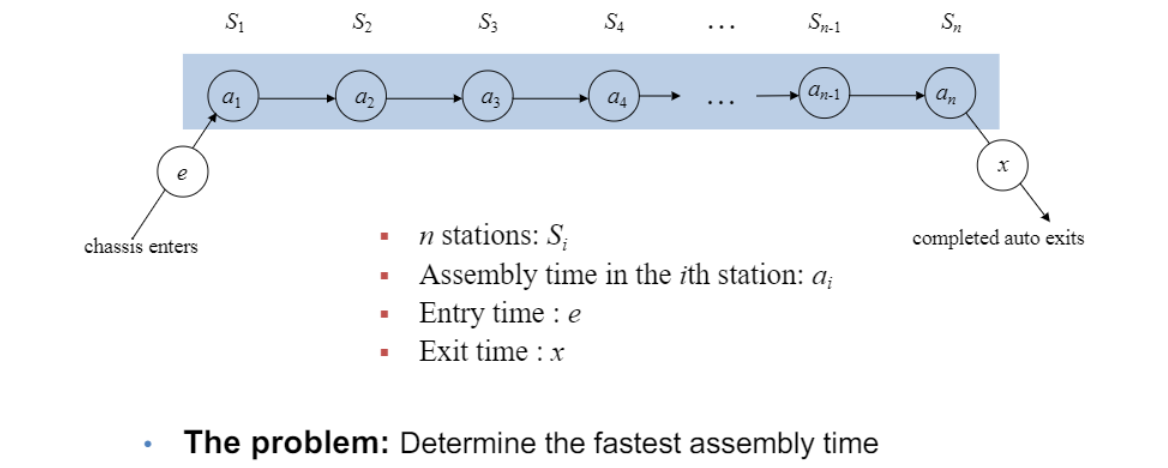1 위와같이 제조 공정 라인이 있을 때 한 라인에는 1부터 n까지 공정이 있음.
이 때 가장 빠른 assembly time 구하는 것이 문제이고,

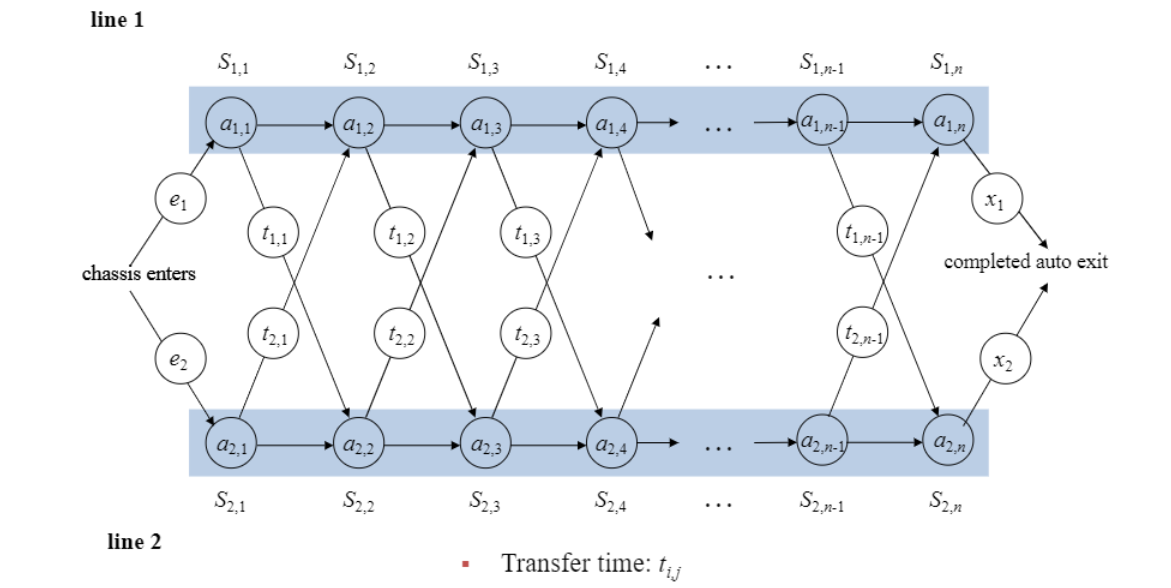2 위와 같이 두 라인이 있을 때
라인에 따라 시간 차이 있고, 다른 라인으로 넘어가는 데에는 시간 t가 존재.

방법1: Brute-force approach

  • 모든 가능한 방법을 계산(가능한 모든 경우의 수 탐색) 후 가장 빠른 길을 찾음
  • $2^n$가지 방법이 있음: 너무 많음

방법2: Dynamic Programming

표를 사용하는 것

3

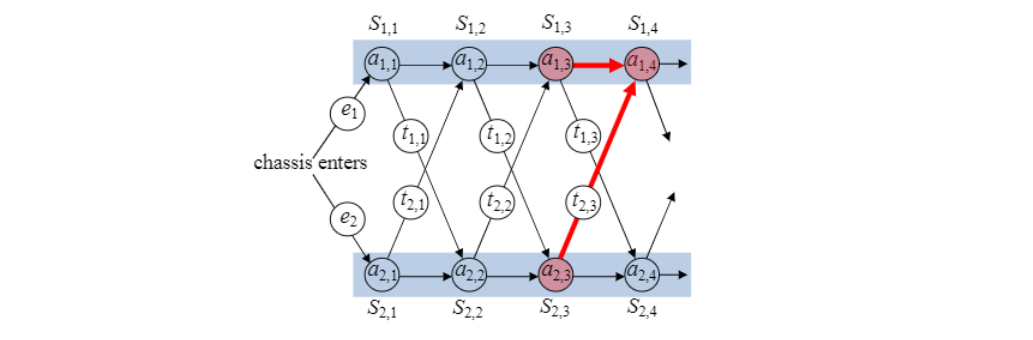
$S_{i,j}$로 가장 빠른 길은 $S_{1,j-1}$ 혹은 $S_{2,j-1}$을 통하는 것

4

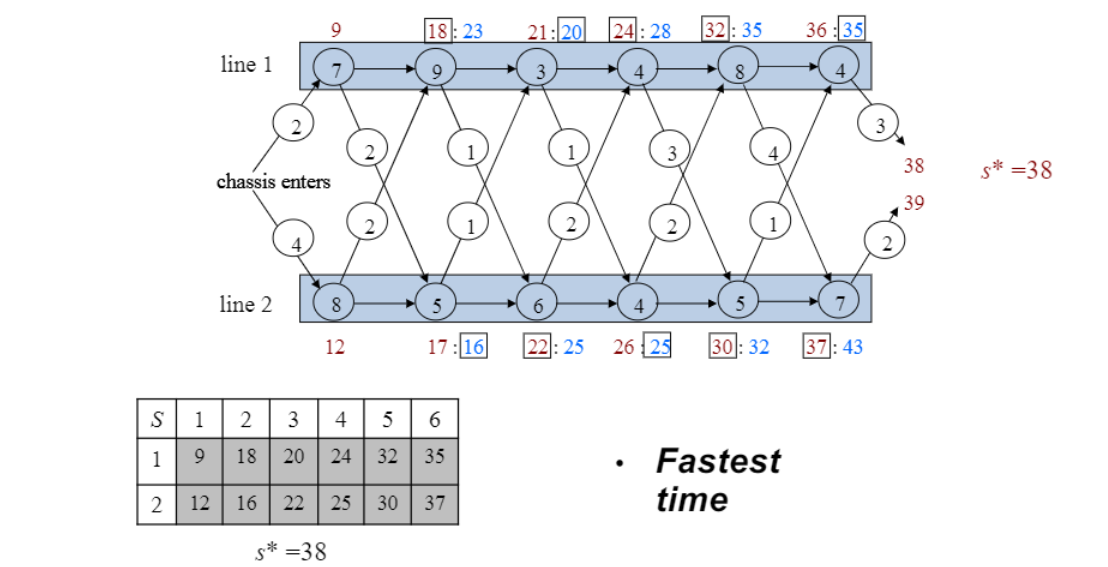
같은 라인에서 넘어왔을 때의 시간과 다른 라인에서 넘어왔을 때의 소요시간을 단계별로 연산.

  • s*는 최종적으로 가장 빠른 시간을 의미
  • 1번 레인, 2번 레인 각각 매 단계별 기존 레인과 넘어오는것 중에서 적은 시간이 걸리는 방법 선택 후 테이블에 작성

5

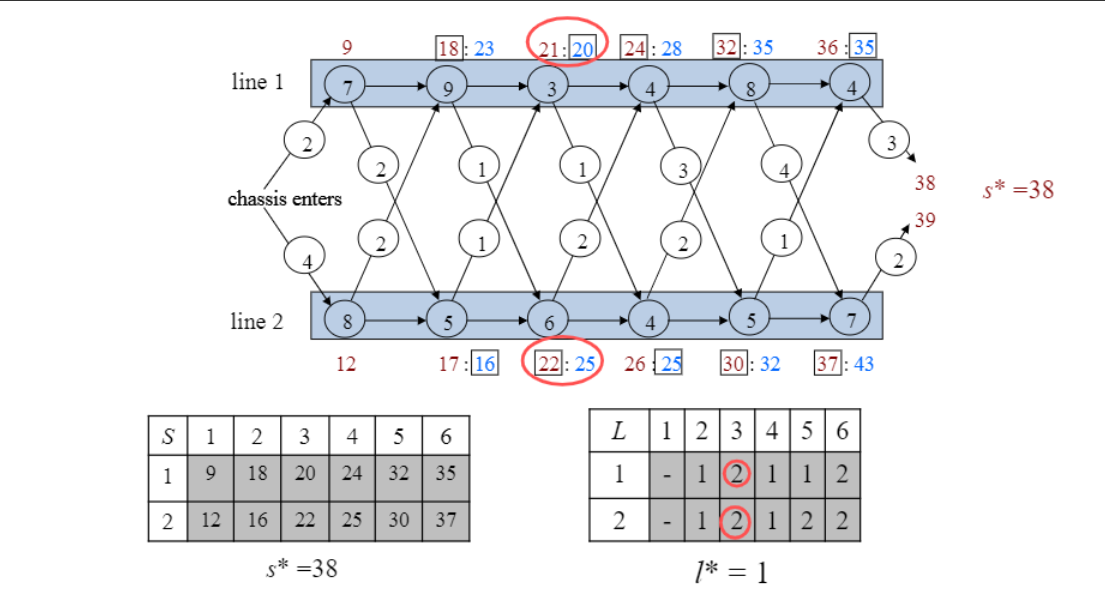
  • 테이블 L에는 더 적은 시간이 걸리게 하는 방법이 어떤 lane을 선택하는것인지 기록.(시간 얼마나 걸렸는지가 아닌 어디를 선택했는지 기록)

6

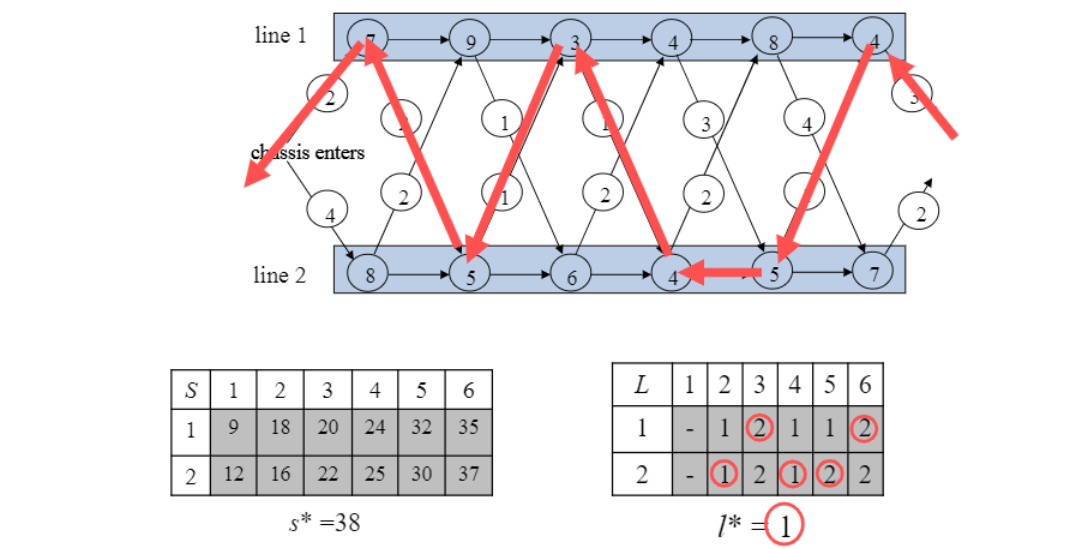
-> 결국 L이라는 table있으면 따라가면 됨. $2^n$아닌 효율적인 방법은 중간 결과 저장해 두는 것

pseudo code

FASTEST-WAY 파라미터:

  • a: station에서 시간
  • t: transfer time
  • e: enter
  • x: exit
  • n: station 개수
FASTEST-WAY(a, t, e, x, n)
    s[1][1] = e[1] + a[1][1] 
    s[2][1] = e[2] + a[2][1] // 각 line에서 station1의 시간
    for j= 2 to n // for문은 constant \theta(n)
        // line 1의 j번째 단계
        if s[1][j−1] ≤ s[2][j−1] +t[2][j−1] // 직전단계 station 1에서 넘어온 경우
            s[1][j] = s[1] [j−1]+a[1][j]
            l[1][j] = 1
        else // 2에서 넘어온 경우
            s[1][j] = s[2][j−1] +t[2][j−1] +a[1][j]
            l[1][j] = 2
        // line 2의 j번째 단계
        if s[2][j−1] ≤ s[1][j−1] +t[1][j−1]
            s[2][j] = s[2][j−1] +a[2][j]
            l[2][j] = 2
        else s[2][j] = s[1][j−1] +t[1][j−1] +a[2][j]
            l[2][j] = 1
    // 최종 결정
    if s[1][n] +x[1] ≤s[2][n] +x[2]
        s* = s[1][n] +x[1]
        l* = 1
    else s* = s[2][n] + x[2]
        l* = 2

PRINT-STATIONS 파라미터:

  • $l:$ table
  • $l^*:$ 맨 마지막에 어디서 나왔는지
  • $n:$ line의 단계 개수
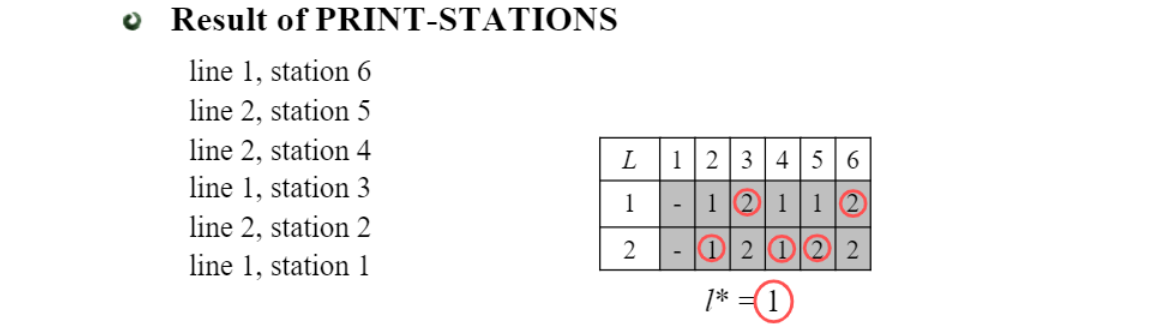
PRINT-STATIONS(l,l*,n)
    i = l*
    print "line"i",station"n // 여기까진 constant
    for j=n down to 2 // n에 비례
        i = l[i][j]
        print "line"i",station"j-1

7

Space consumption

  • Table $s: 2n$
  • Table $l: 2n$
  • $\theta(n)$

-> 시간 절약 but 공간 사용 많음

Running time

  • 각 요소 연산하는데 $\theta(1)$시간 소요
  • 전체는 $\theta(n)$

최소 시간만 알면 되는 경우(fastest time only)

최소 시간만 알면 된다면, table l은 필요 X
(L은 되짚어 가는데 필요한 table)

  • $\theta(1)$ space
    • table $l:$ 필요 X
    • table $s:$ 2n개 -> 4개만 있으면 됨 (이전것으로 다음것 구해나가기)

=> $2^n$ 걸리는 것을 $\theta(n)$으로 해결 가능

  Space Time
Assembly-line scheduling $\theta(n)$ $\theta(n)$
Rod cutting    
Longest common subsequence    
Matrix-chain multiplication    

출처 : 2023-2 ITE2039 수업

참고: https://doorbw.tistory.com/42