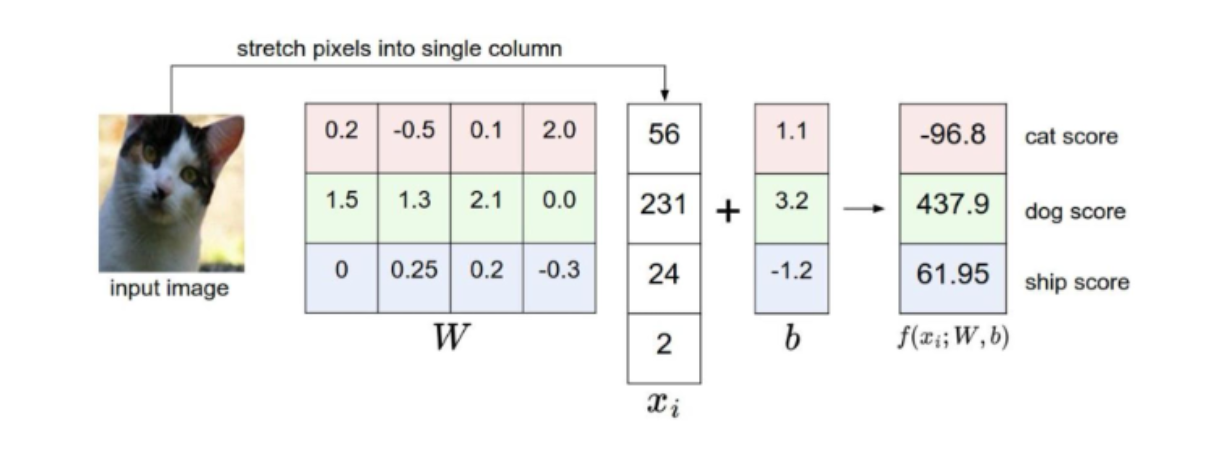
Linear Classifier

: 선을 이용하여 집단을 두개 이상으로 분류하는 모델 \(f(x_{i},W,b) = Wx_{i}+b\)

matrix size example:

$f(x_{i},W,b)$ : 10 x 1

$W$ : 10 x 3072
$x_{i}$ : 3072 x 1
　　= 32x32x3(이미지 1개) x 1
$b$ : 10 x 1

input, output:

input으로 $x_{i}$ 이미지 넣으면 $\to$ output으로 각 class 별 score인 10개의 수

1

이러한 classifier가 내놓은 결과값에 대해 평가하기 위해 정답 레이블과 비교.
이때 비교해주는 함수가 Loss function

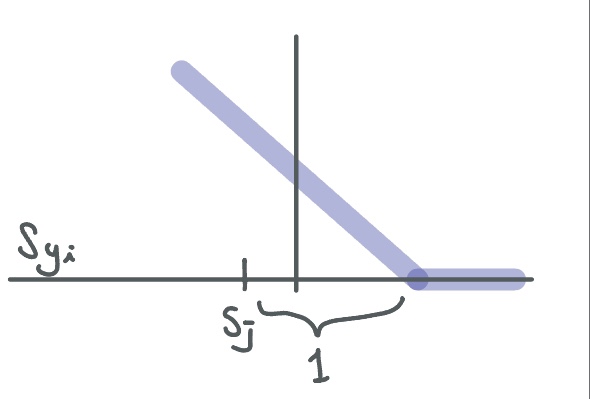
Multiclass SVM Loss (= hinge loss)

\[L_{i} = \begin{Bmatrix}0 　　 (if S_{y_{i}} \geq S_{j} + 1) \\ S_{j} - S_{y_{i}} + 1　(othersise)\\ \end{Bmatrix}\] \[= \sum_{j\neq y_{i}} max(0, S_{j} - S_{y_{i}} + 1)\]

$S_{j}$ : 오답 카테고리의 score
$S_{y_{i}}$ : 정답 카테고리의 score

정답 score가 오답score보다 safty margin인 1보다 크면 loss가 0
즉 좋은 output이라는 것

그리고 위의 조건이 아니라면, 오답 score - 정답 score + 1을 loss로

결국 얼마나 안좋은지를 나타내는 수치

그리고 이를 그래프로 나타내면

2

예시)

cat, car, frog 이미지를 넣고 이 3가지 class에 대한 score를 가지고 SVM loss 계산

  고양이 이미지 자동차 이미지 개구리 이미지
cat 3.2 1.3 2.2
car 5.1 4.9 2.5
frog -1.7 2.0 -3.1

고양이 이미지를 넣은 경우,
cat class의 점수가 가장 높아야 하는데 car class의 점수가 가장 높다.
따라서 loss 가지게 됨.

먼저 cat와 car로 loss 계산을 해보면,
$S_{j} - S_{y_{i}} + 1$
= (오답인 car) - (정답인 cat) + 1
= 5.1 - 3.2 + 1

cat과 frog를 보면,
cat이 3.2, frog가 -1.7이다.
cat이 1 이상 크기 때문에 loss가 0

따라서 cat의 loss인 $\sum_{j\neq y_{i}} max(0, S_{j} - S_{y_{i}} + 1)$ 는
2.9 + 0 이다.

+ 자동차는 0
+ 개구리는 6.3 + 6.6 = 12.9

각각의 $L_{i}$ 들로 최종 $L$을 구하면, \(L = \frac{1}{N} \sum_{i=1}^N L_{i}\)
$L = (2.9 + 0 + 12.9)/3$ $5.27$

hinge loss의 특징

  • 데이터에 민감하지 않다. score의 점수보다 정답이 오답보다 높은지가 중점
  • 최소 0, 최대 $\infty$
  • $W$ 값이 작아 score 자체가 작아지는 경우에도 마지막에 더하는 1이 있어서 0의 근사치가 나오더라도 Loss 자체가 무한히 작아지지 않음 (sanity check)

Softmax Classifier

계산법

  1. softmax 함수를 거쳐 class별 확률을 계산
    \(P(Y = k | X = x_{i}) = \frac{e^sj}{\sum_{j}e^s j}\)

    모든 스코어 exp 취한것의 합으로 해당 class의 스코어에 exp 한 것을 나눔
    = 확률

    0~1 사이의 값, 모든 확률의 합은 1

  2. 이후 확률값과 실제값 비교 \(L_{i} = - \log {P(Y = y_{i} | X = x_{i})}\)

    위의 값에 -log 취해주어 loss 구함

특징

  • 정답점수만 높으면 상관없던 hinge loss(점수에 둔감)와 달리
    확률로 계산되기 때문에 데이터 변경되면 값에 영향을 미침.
    따라서 데이터에 민감함

W 값이 너무 오버피팅 되는 경우 방지하기 위한 Regularization과
최적의 W 찾는 Optimization은 다음 post에

출처1 : 2023-1 ITE4052 수업
출처2