Contents

  • Graphs(part1)
    • Graph basics
    • Graph representation
      • Adjacency-list representation
      • Adjacency-matrix representation
  • Searching a graph (part2)
    • Breadth-first search
    • Depth-first search
  • Applications of depth-first search(part3)
    • Topological sort

Elementary Graph Algorithms 2

  • Distance :
    u(노드1)부터 v(노드2)까지 가장 짧은 path의 edge의 개수

Breadth = 폭

  • Graph $G = (V,E)$와 Source vertex $s$가 주어졌을 때, $s$로부터 도달할 수 있는(reachable) 모든 vertex “discover”

  • Source $s$로부터 distance가 증가하는 순서로 vertices를 discover

    • distance 1인 모든 vertex들 discover 후, distance 2인 것 discover …

Example:

Step 1 1

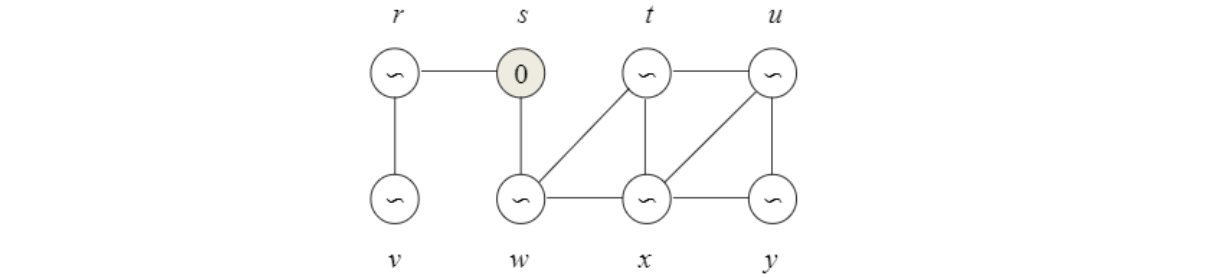
Source인 $s$에서 시작.

Step 2 2

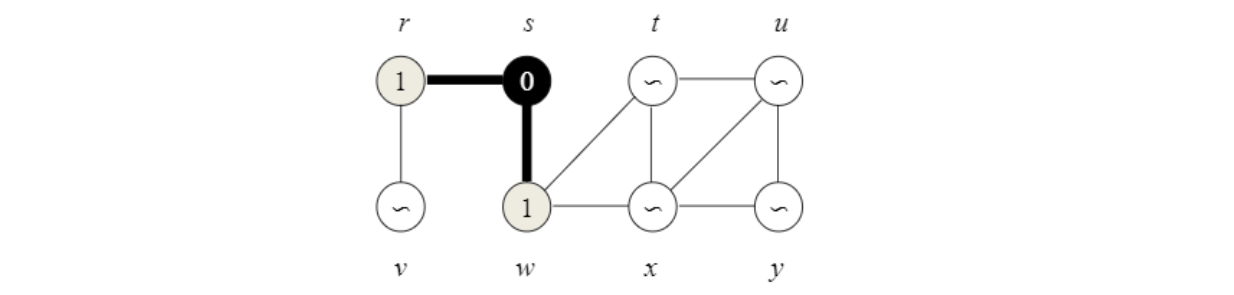
$s$에서 distance가 1인 것들 먼저 전부 탐색

Step 3 3

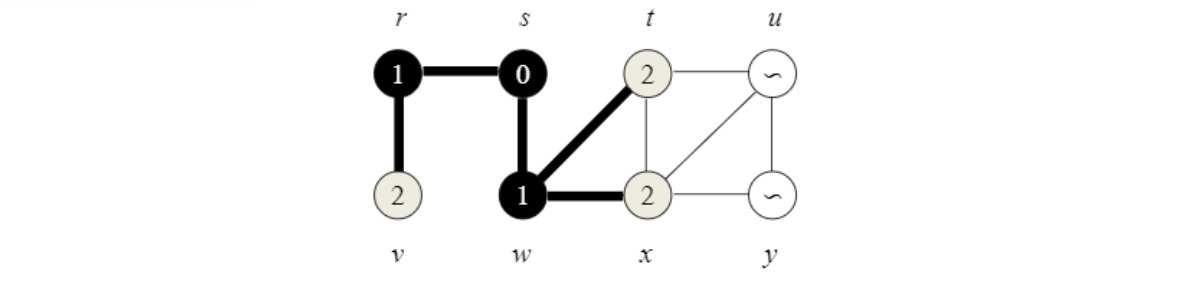
t의 adjacent 중에 어딜 가야 할지 알려주는 것이 색깔.
t의 adjacent w, x, u 중에서 불필요하게 w갈 필요 X

Step 4 4

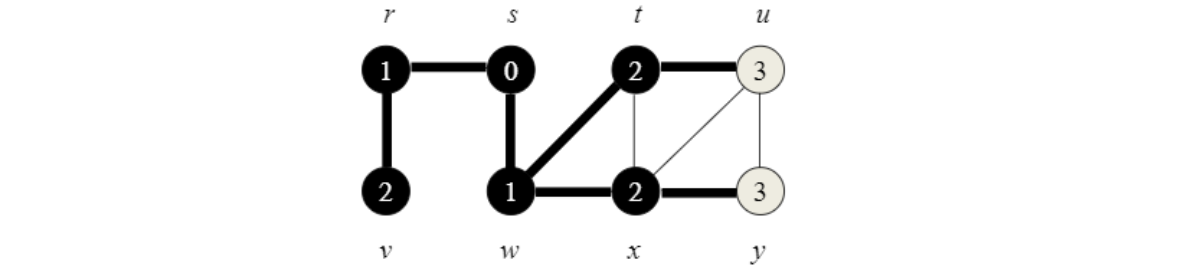
Step 5 5

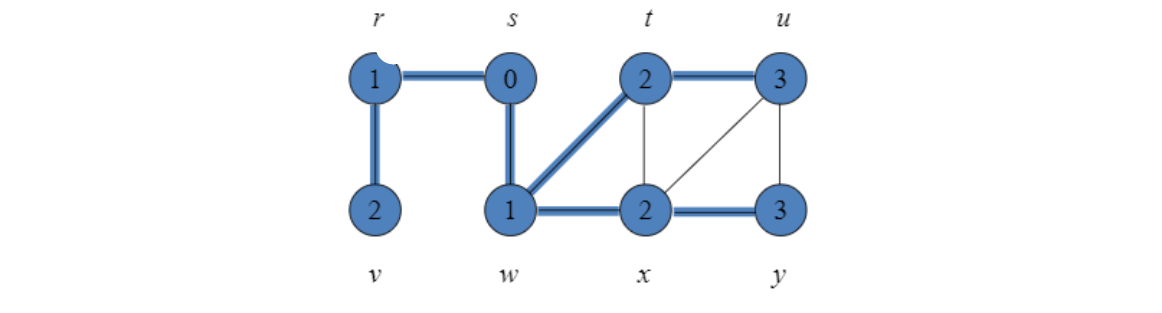
위 과정을 통해 추가적으로 얻을 수 있는 것들:

  • source 로부터의 distance
    ex.) $u.d=3$

  • vertices의 predecessor
    $u.\pi = t$

  • G의 Predecessor subgraph
    = $ G_\pi= (V_\pi, E_\pi)$

    • $V_\pi= {v ∈V \vert v.\pi≠ NIL}$ $ U { s}$

    • $E_\pi= {(v.π, v) \vert v ∈V_\pi-{s}}$

    • predecessor subgraph $G_\pi$는 breadth-first tree

      • $\because$ 연결되어있고 $\vert E_\pi\vert =\vert V_\pi\vert -1$
      • $E_\pi$의 edge들은 tree edges 라고 불림
BFS(G, s)
    // part1: Initialization
    for each vertex u ∈ G.V ─ {s}
        u.color = WHITE     // 처음 white로 initialize
        u.d = ∞
        u.π = NIL
        s.color = GRAY
    s.d = 0
    s.π = NIL
    Q = Ø   //우리가 사용할 자료구조
    ENQUEUE(Q, s)
    // part2: Graph Explorarion
    while Q ≠ Ø     // 여기서 색깔 쓰임
        u = DEQUEUE(Q)
        for each v ∈G.Adj[u]
            if  v.color== WHITE
                v.color= GRAY
                v.d= u.d+ 1
                v.π= u
                ENQUEUE(Q, v)
        u.color= BLACK      // Q가 empty 나면 BLACK

6

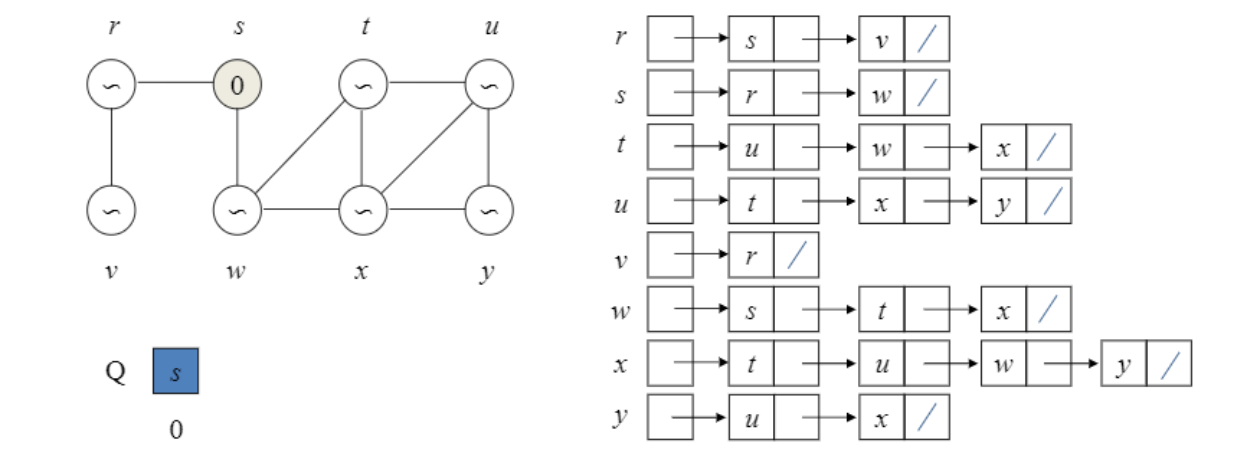
adjacent 노드 만나면 Q에 넣음. 그 노드의 adjacent 들을 탐색하기 직전 Q에서 제거.
Ex) 처음에 s있고, 탐색 시 s 빼줌. 새로운 adjacent인 r과 w를 만날때 Q에

  • white : discovered 되지 않은 것. (Q에 enter 하지 X)
    = 방문된적 없는 노드

  • gray : discovered (Q에 있음)
    = 그 노드는 방문됨, adjacent 한 주변 node 안가봄

  • black : finished (out of the Q)
    = adjacent까지 다 가봄

  • Running time

    • Initialization (part1) : $\theta(V)$
    • Exploring Graph (part2) : $O(V+E)$
      • vertex는 최대 한번 examined
      • edge는 최대 두번 explored

    => $O(V+E)$

Colors of vertices

  • 초기에 모든 노드는 WHITE (not discovered)
  • Discovered 되면 GRAY
  • Adjacency가 전부 examined 되었다면 finish 된 것. 이는 BLACK

Timestamps

각 vertex마다 두 timestamp가 있다

  • $v.d$ : discovery time (gray 될때)
  • $v.f$ : finishing time (black 될때)

7

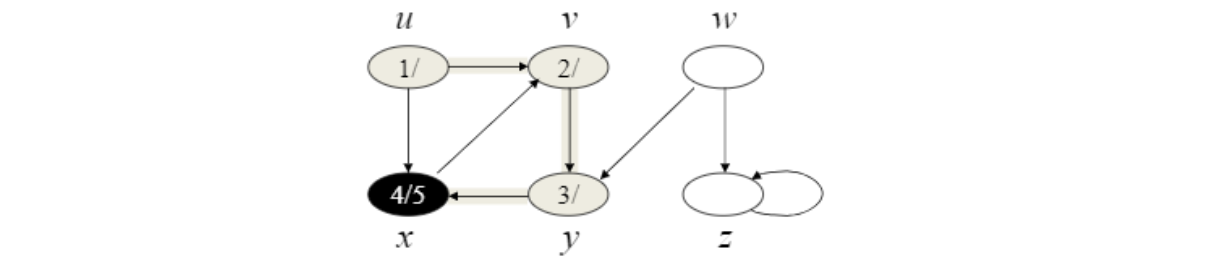
Pseudo code

DFS(G)
1   for each vertex u ∈ G.V
2       u.color = WHITE
3       u.π = NIL
4   time= 0
5   for each vertex u ∈G.V
6       if u.color == WHITE
7           DFS-VISIT(G,u)

DFS-VISIT(G,u)
1   time= time + 1
2   u.d = time
3   u.color= GRAY
4   for each v ∈ G.Adj[u]
5       ifv.color == WHITE
6           v.π = u
7           DFS-VISIT(G,v)
8   u.color = BLACK
9   time=time+ 1
10  u.f= time

Running time

pseudo code에서,

DFS(G): line1~4 -> Initialization
$\Theta (V)$
DFS(G): line5~7 -> Graph Exploration
$\Theta (V+E)$
DFS-VISIT(G,u)
$\Theta (E)$

Total => $\Theta(V+E)$

(디테일들 많이 SKIP)

출처 : 2023-2 ITE2039 수업