다루는 algorithms

  • Generic MST
  • Prim’s Algorithm
  • Kruskal’s Algotrithm

Minimum Spanning Trees

이전까지 기본적인 Graph 알고리즘 (DFS, BFS 두가지) 봤었음.

Weighted Undirected Graphs

도로망, network 등 isolation 없는 connectivity를 보기 위한 알고리즘인 경우가 많아($\because$ application이 보통) 보통 undirected graph

  • Weighted undirected graph $G=(V,E)$
    • 각 edge $(u,v)\in E$ 에 대해, weight $w(u,v)$가 있다

    1

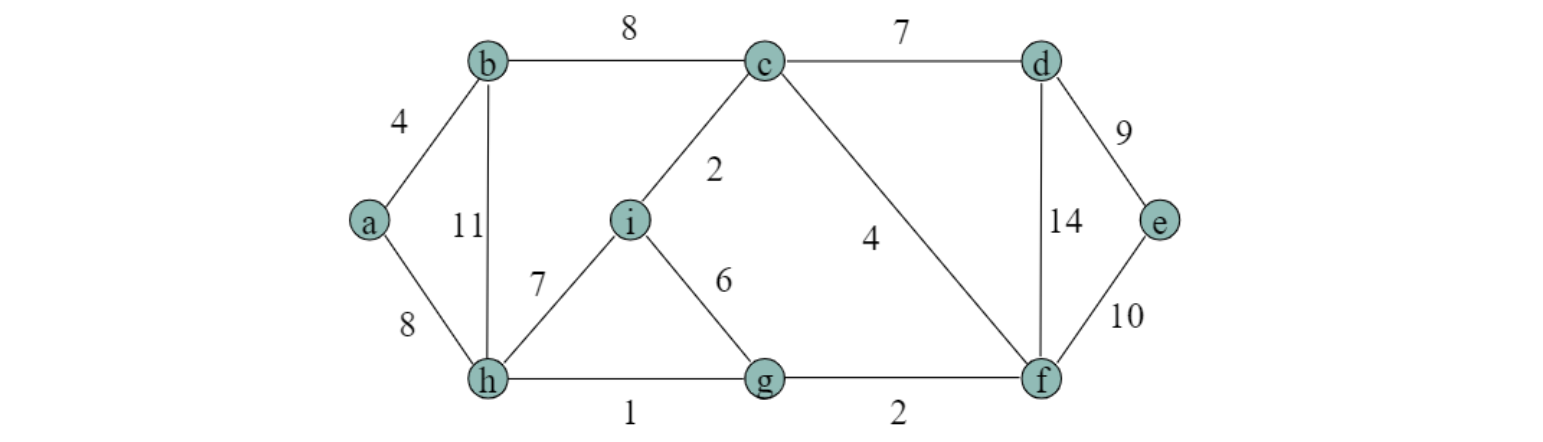
Spanning Trees

  • A spanning tree for G
    • tree가 되게 하는 그래프 G의 edge들 중의 subset. = spanning tree
    • ‘spanning’ tree 란 모든 node cover 하는 tree에 해당하는 tree.
    • 여러개가 될 수 있음. 그런데 우리가 원하는 것은 cost가 제일 적은 것(edge의 weigh들의 합)을 원함.

    2

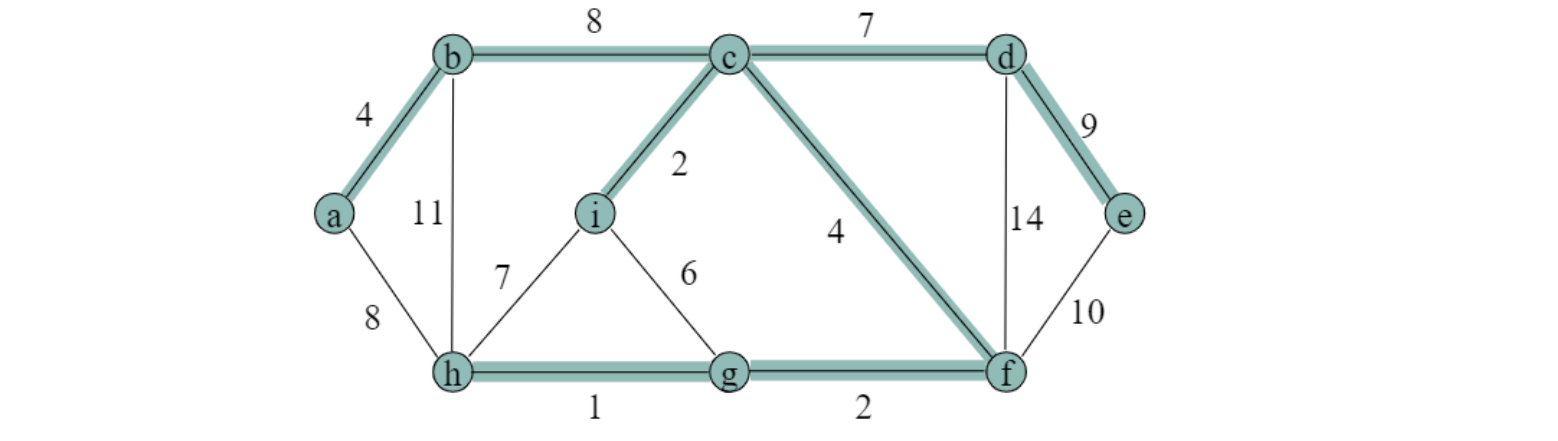
Minimum Spanning Trees

  • Cost
    $w(T) =\sum_{(u,v)\in T} w(u,v) $

  • Minimum-Spanning-Tree problem

    • 가장 cost가 작은 spanning tree 찾는 것
    • $T$가 acyclic하면서 모든 vertex를 connect -> tree (이전에 배운 tree의 조건)

Minimum spanning tree를 구하는 대표적인 두 알고리즘이 있는데 둘이 다른 것 같지만 generalize 해서 보면 같은 알고리즘 처럼 생각할 수 있음
MST 2가지 있는데 abstract 뽑은게 generic-MST.
special case 2가지가 1) Prim’s Algorithm, 2) Kruskal’s Algorithm

Generic-MST

GENERIC-MST(G, w)
    A = Ø # empty에서 시작해서 spanning tree될 때 까지 edge 추가하기
    while A does not form a spanning tree
        do find an edge(u, v) that is safe for A
        A = A ∪ {(u, v)}
    return A

Safe edge란? (이 부분이 각 알고리즘마다 조금씩 다름)
ex) cycle 안만들고, minimum

  • generic MST에서 safe edge란 subset A에 (u,v)추가했을 때 여전히 minimum spanning tree의 subset.

Prim’s Algorithm

기본 개념은, edge의 set을 증가시키는 것이 아니라 node의 set을 추가시키는 것이다.

그런데 어차피 node의 set을 증가시킬때 그 노드가 기존의 node와 어떤 edge로 연결되게 추가시키기 때문에 edge 추가하는것과 같은 이야기.

cost도 edge 추가시킬 댸 더하는 cost를 node의 cost 처럼 더하기에 동일방식

동작방식

STEP 1

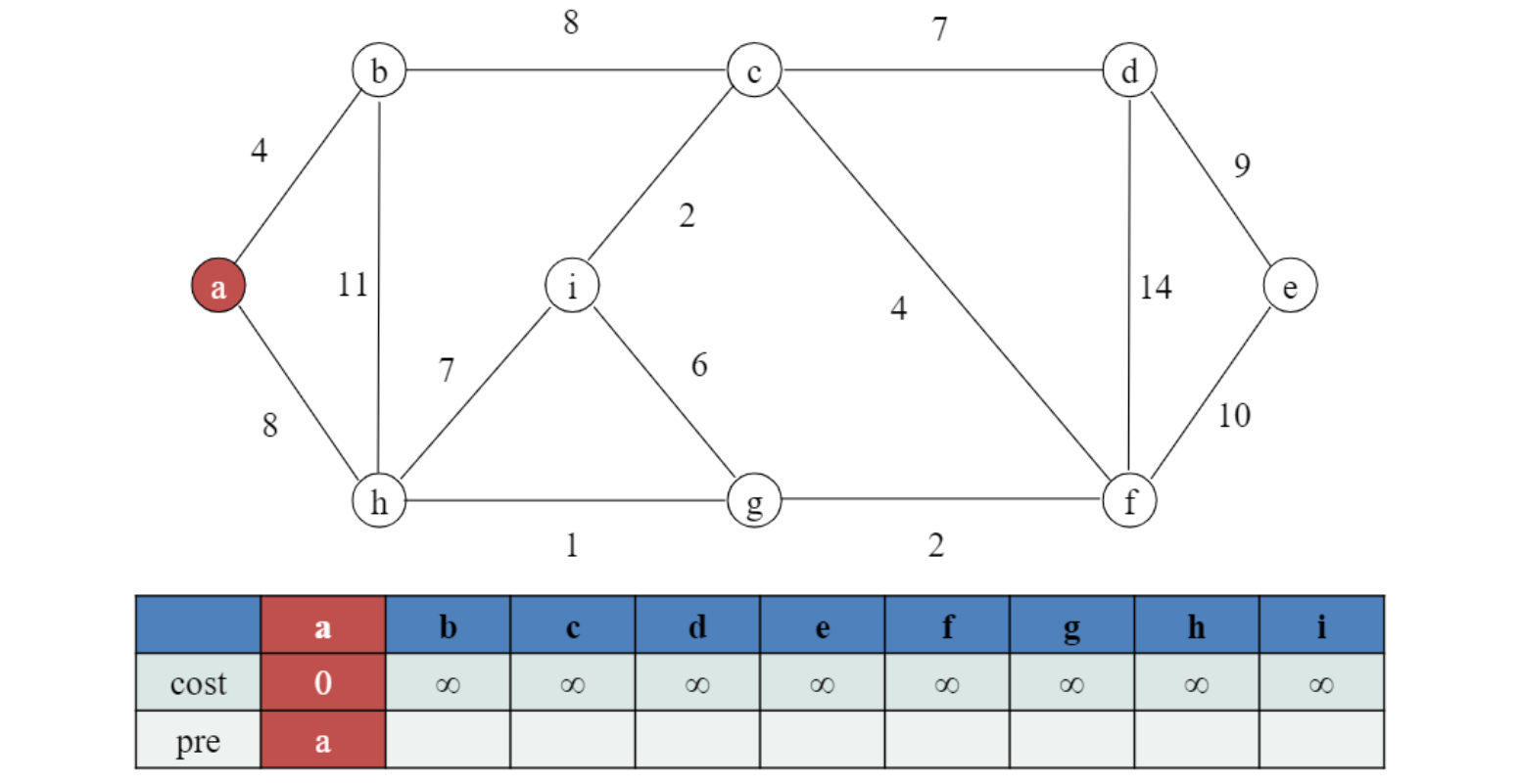3 initially 초기화.
임의의 노드 a에서 시작.
나머지 모든 노드는 minimum spanning tree에 들어가지 않았기 때문에 모르니까 $\infin$

pre : predecessor에 해당하는 노드 표기
결국 edge 나타내는 것.

STEP 2

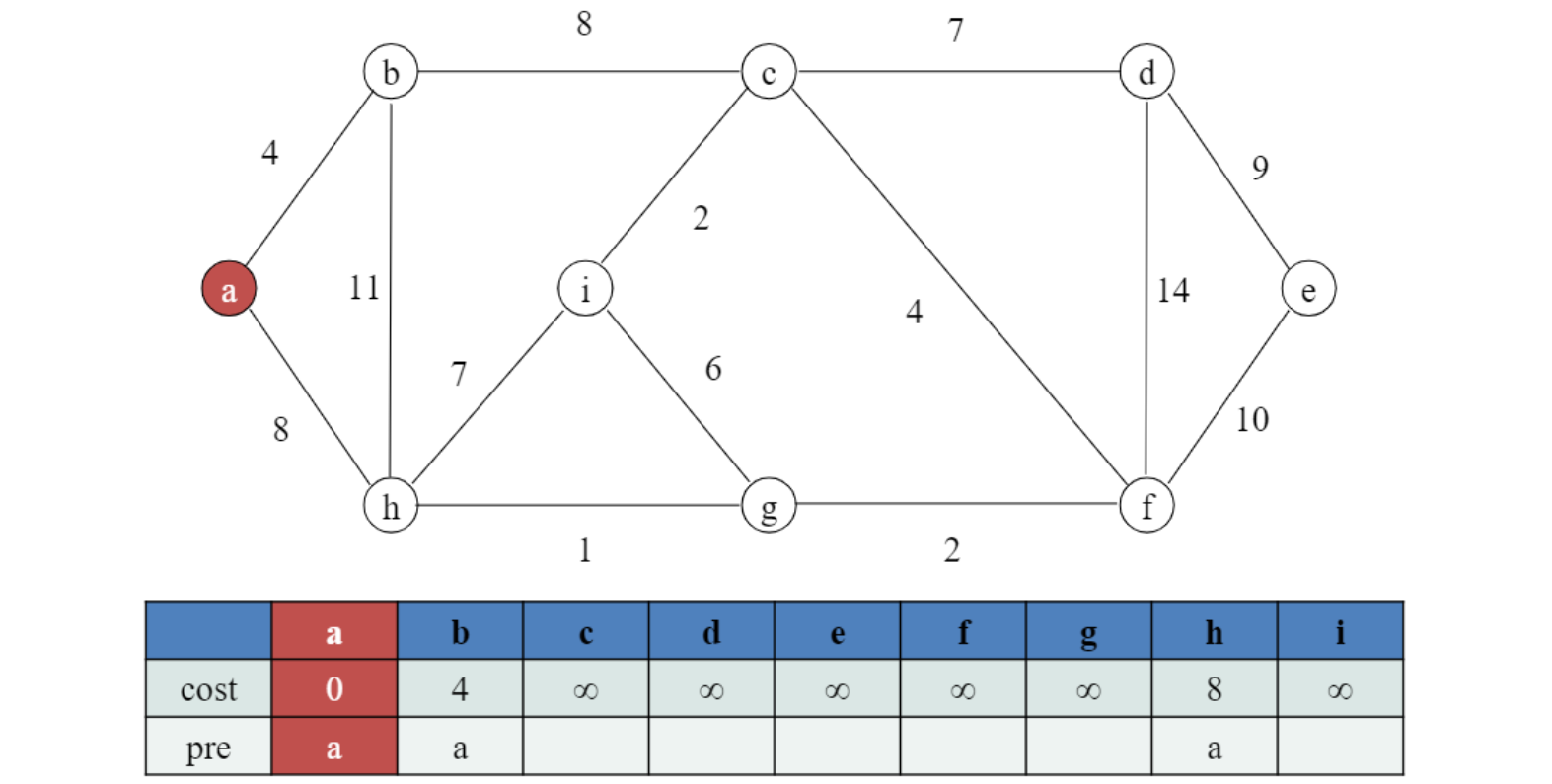4 이후 a와 연결된 모든 adjacent한 모든 edge 살펴봄.

cost, pre update

예시의 경우 b와 h까지의 cost가 $\infin$에서 4와 8로 update

전체에서 cost 가장 작은것을 선택.

위 예시의 경우, node b가 선택됨.
(node h의 cost와 predecessor 기록 되는 것도 잊지 말기)

STEP 3

5

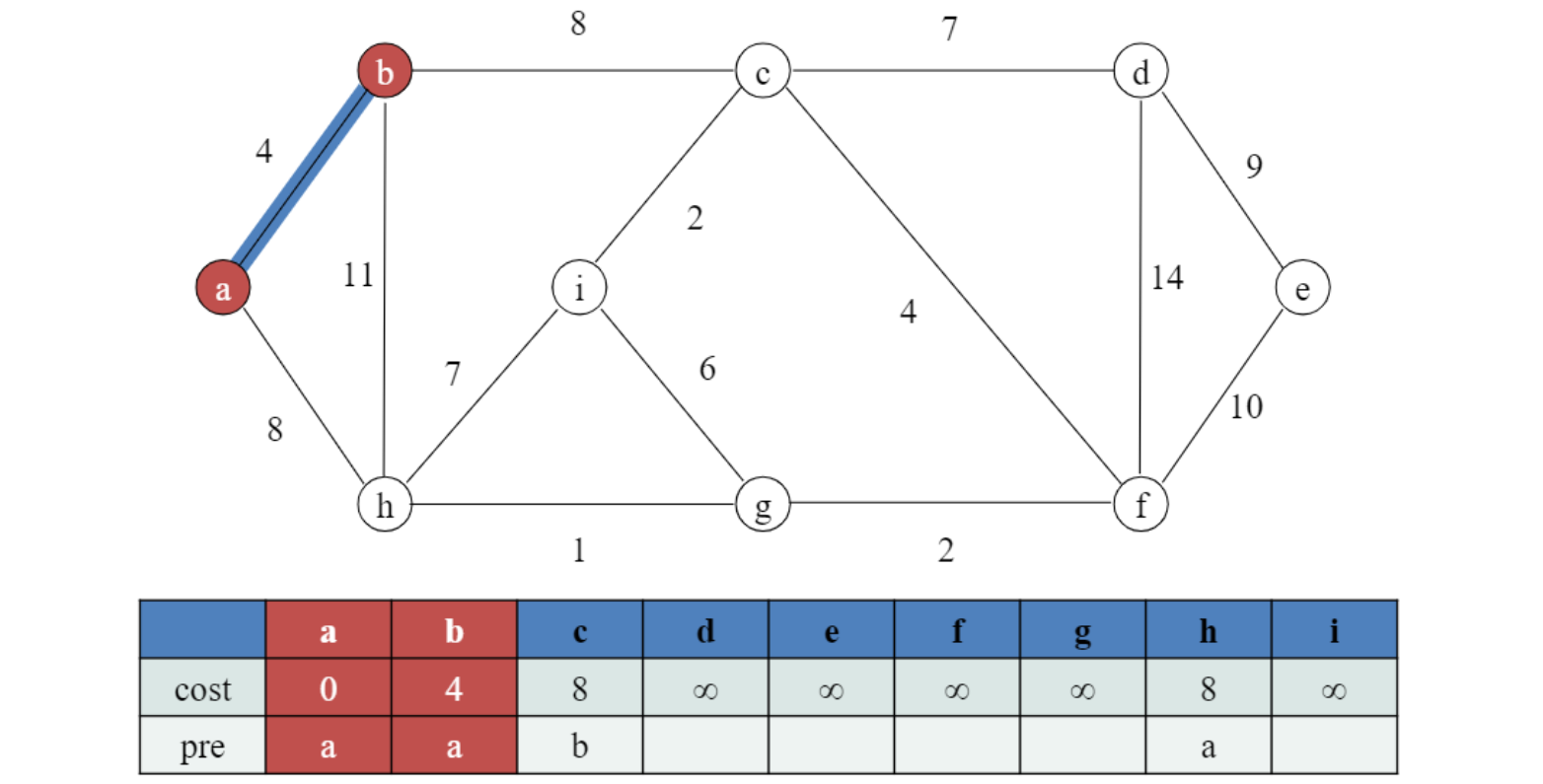
다시 선택된 노드를 기준으로 adjacent 살펴보고,

cost 작은것 update.

예시의 경우 h는 기존 경로가 cost가 적기 때문에 c만 update.

이후 전체에서 cost가장 작은것 선정

6

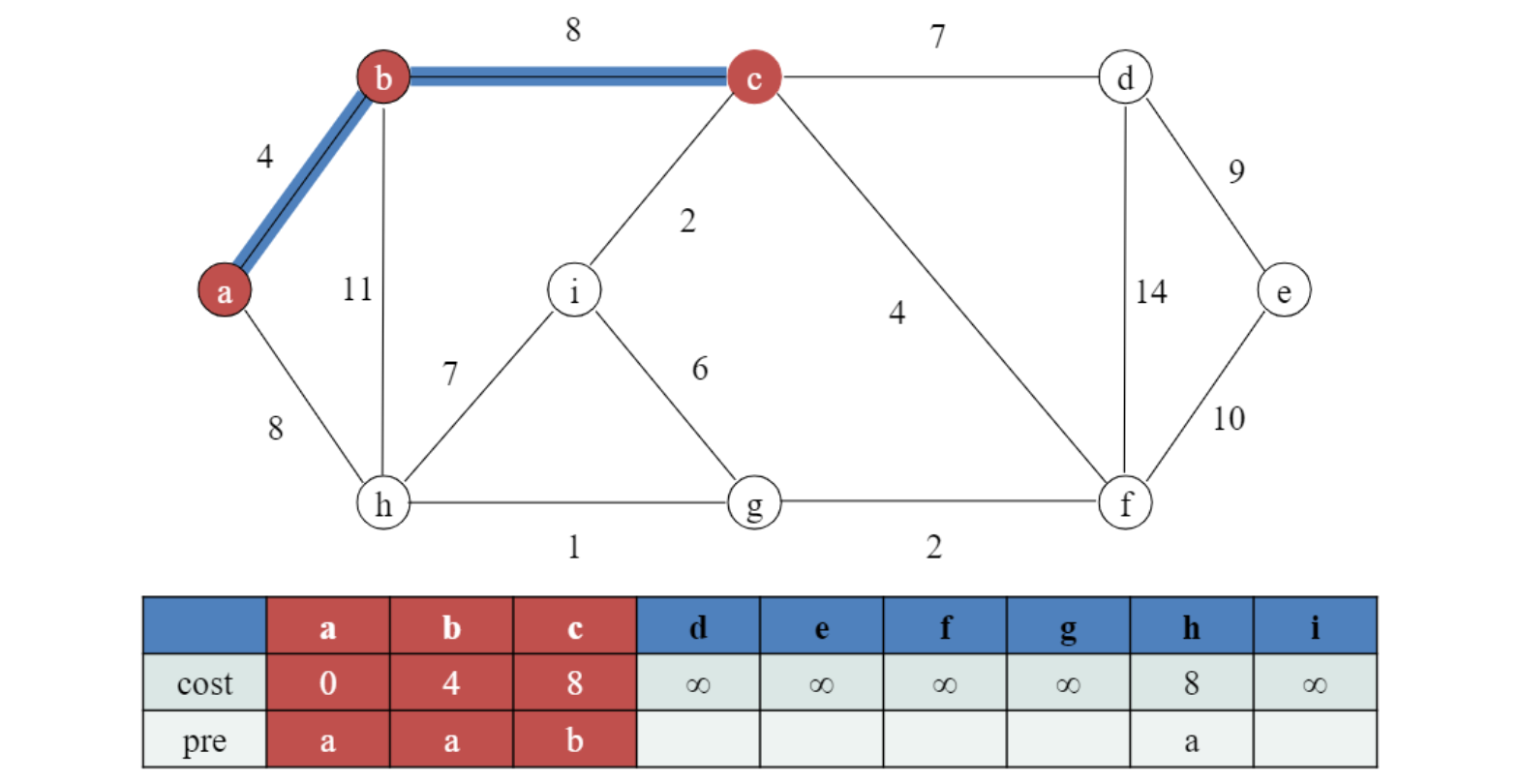
이러한 과정 반복

STEP 4

7

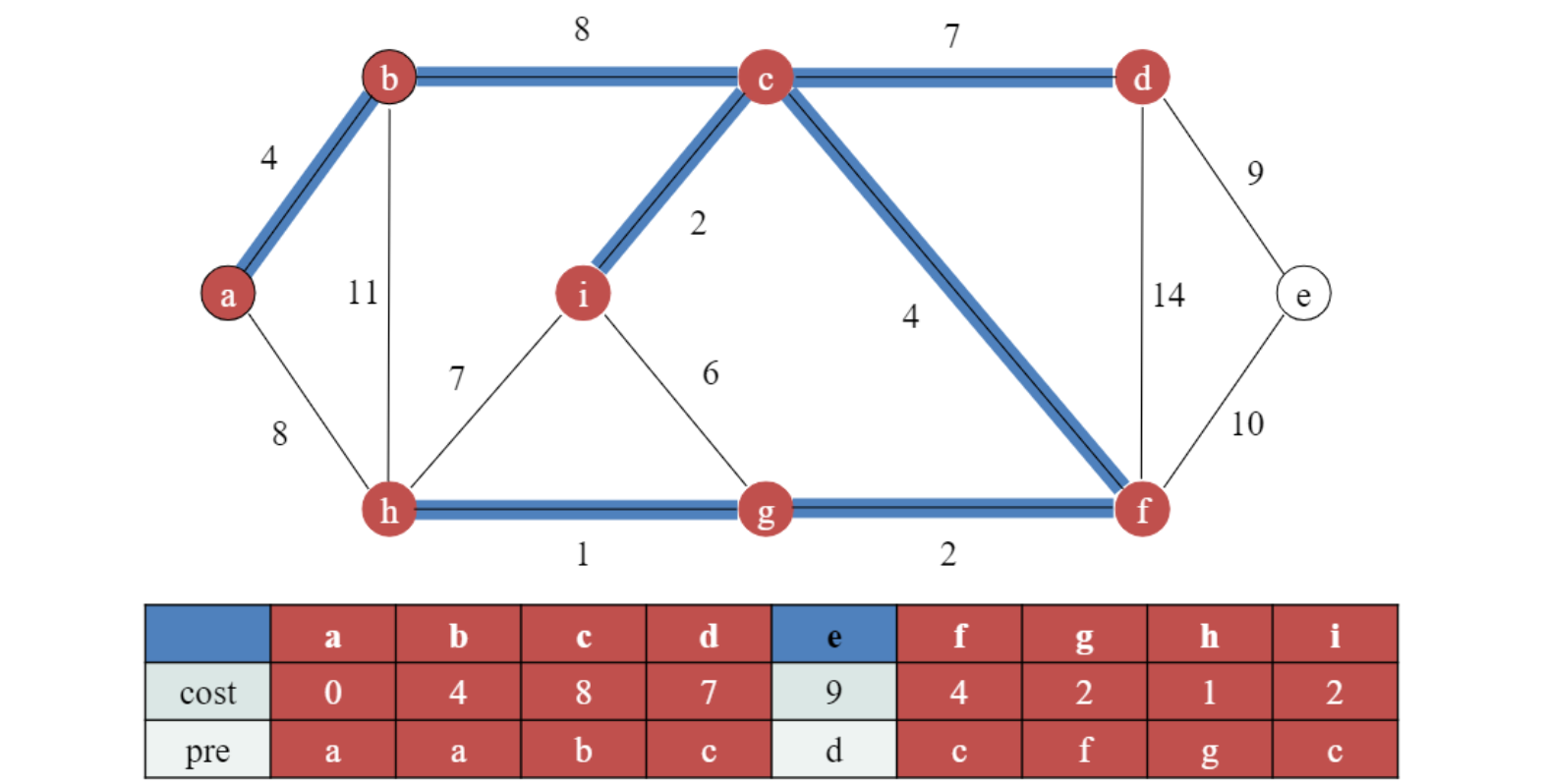
노드들 전부 선택된 후에 (남아있는 노드 없다면) 종료

8

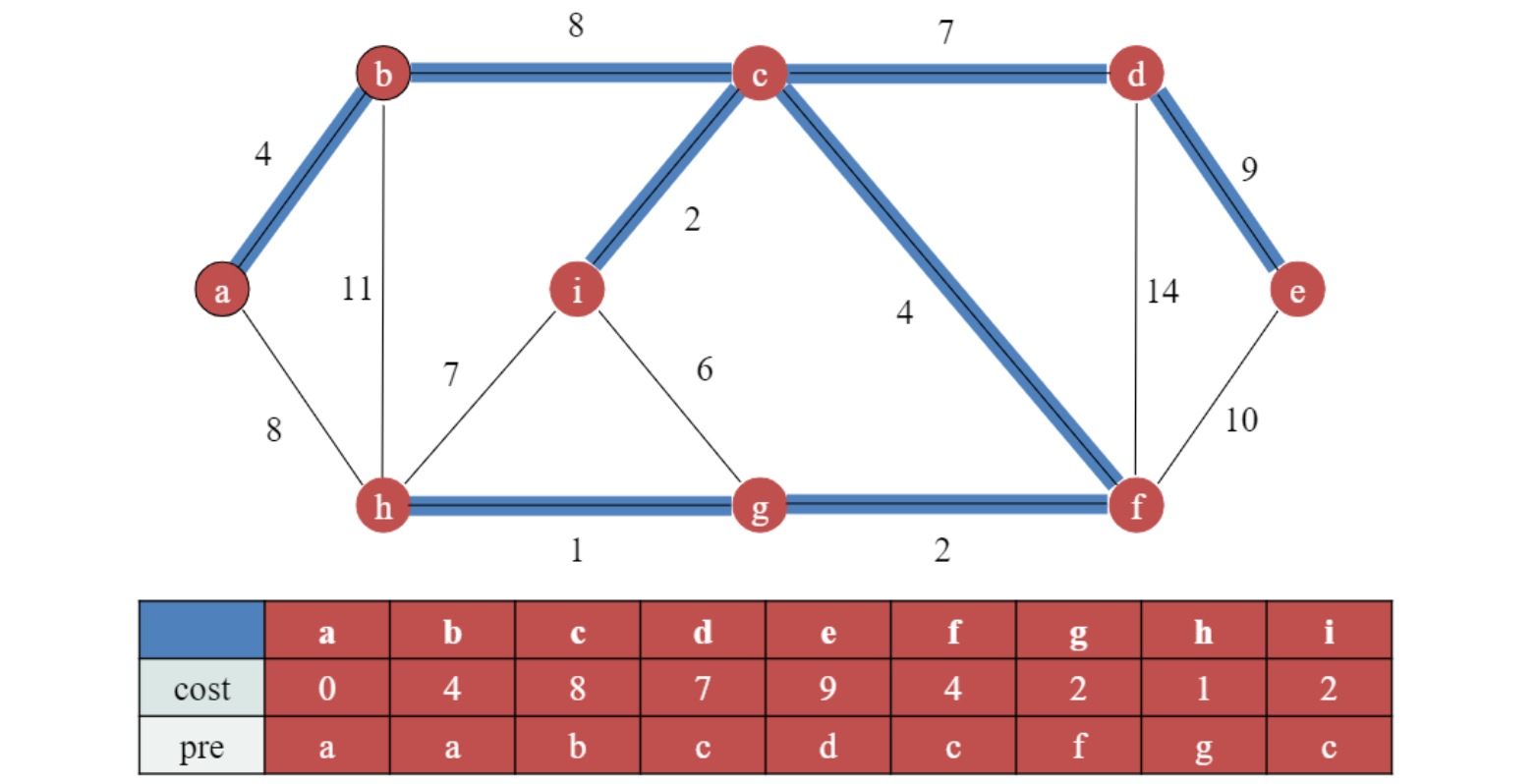
✏️ BFS와 유사.   
BFS는 distance가 cost와 유사하지만,   
시작노드에서 그 노드까지 가는 거리를 더하지만, 여기서는 그 edge가 tree에 포함될때 그 edge의 cost만 봄   
하지만 기본적인 방식은 가장 작은 것 하나를 먼저 뽑고, adjacent들 처리하고, 다시 집어넣고 ...    
나중에보면 '다익스트라'랑도 유사
자료구조

결국 남아있는것들 중 cost가 제일 작은것을 뽑기에 **Binary heap** 쓰는것이 자연스러움

과정은 동일

STEP 1

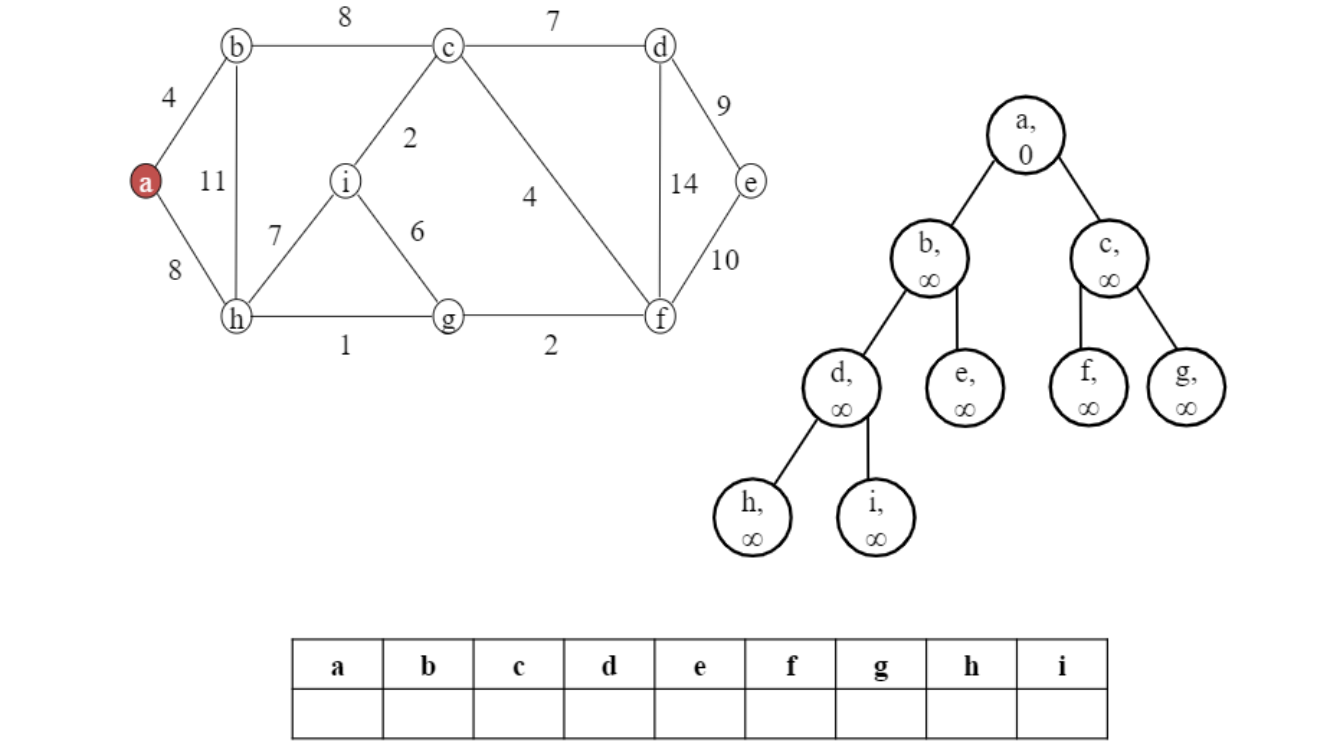9 처음에 전체 노드를 대상으로 BUILD HEAP
시작노드 하나만 cost가 0, 나머지는 $\infin$

이후 EXTRACT-MIN

위 예시에선, a가 빠지고 그 자리에 i들어감. 그리고 MIN-HEAPIFY

STEP 2

10

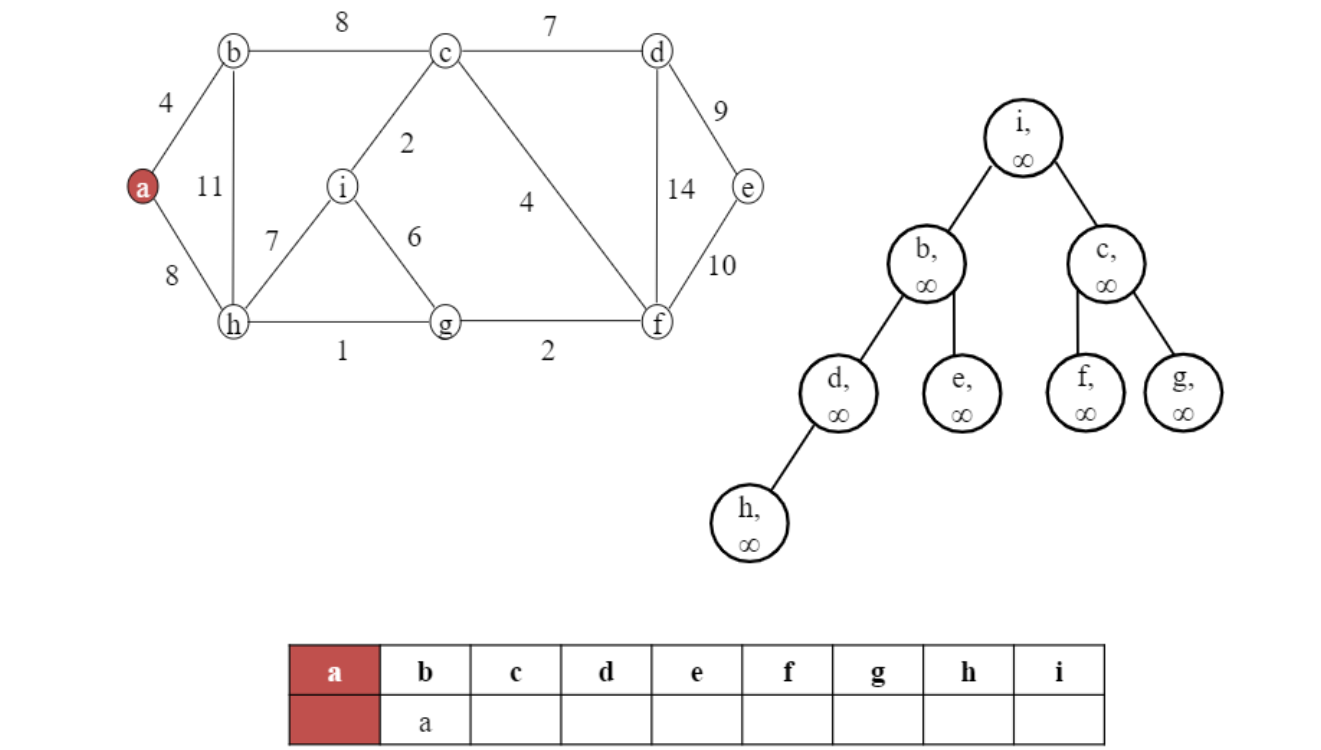
EXTRACT-MIN과 MIN-HEAPIFY외에 adjacent 한 cost로 update위한 DECREASE-KEY(x,y) operation 필요.

값 update 하고 MIN-HEAPIFY

11

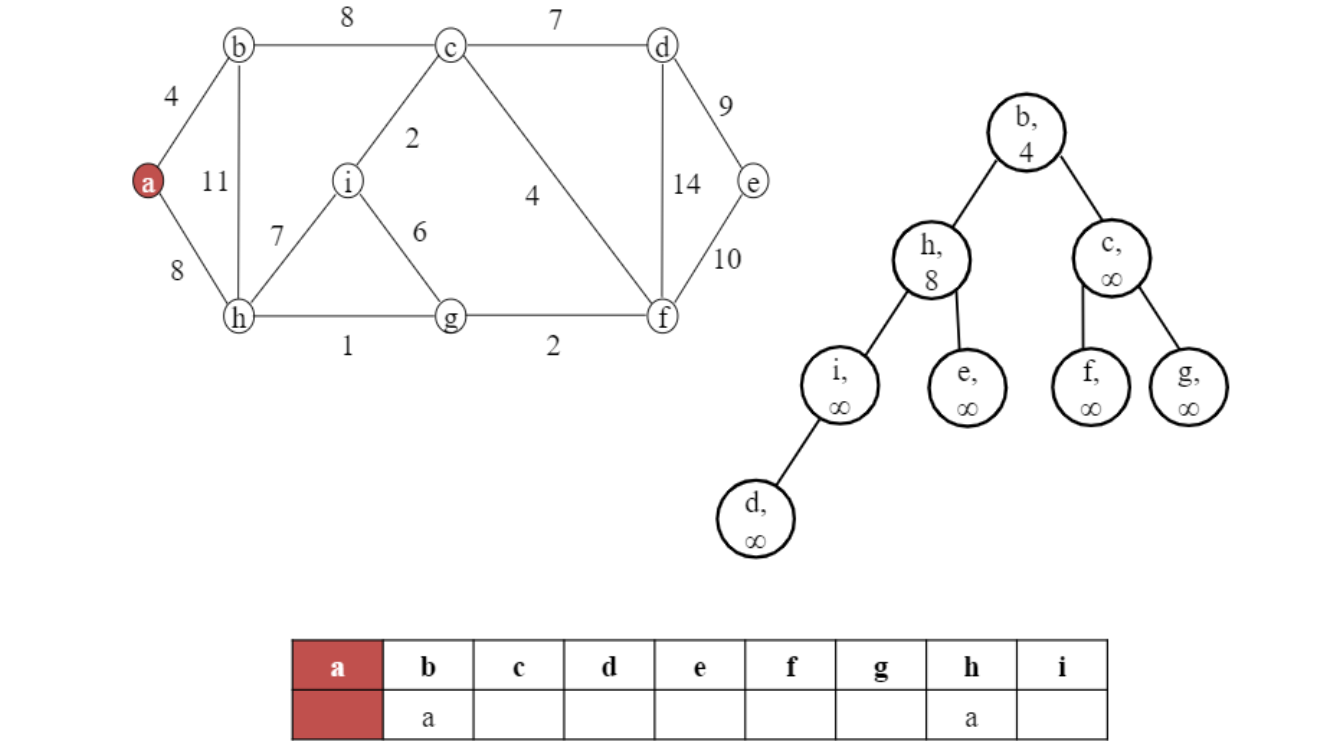
위 예시에선 b를 4, h를 8로 update한 후 MIN-HEAPIFY

STEP 3

12

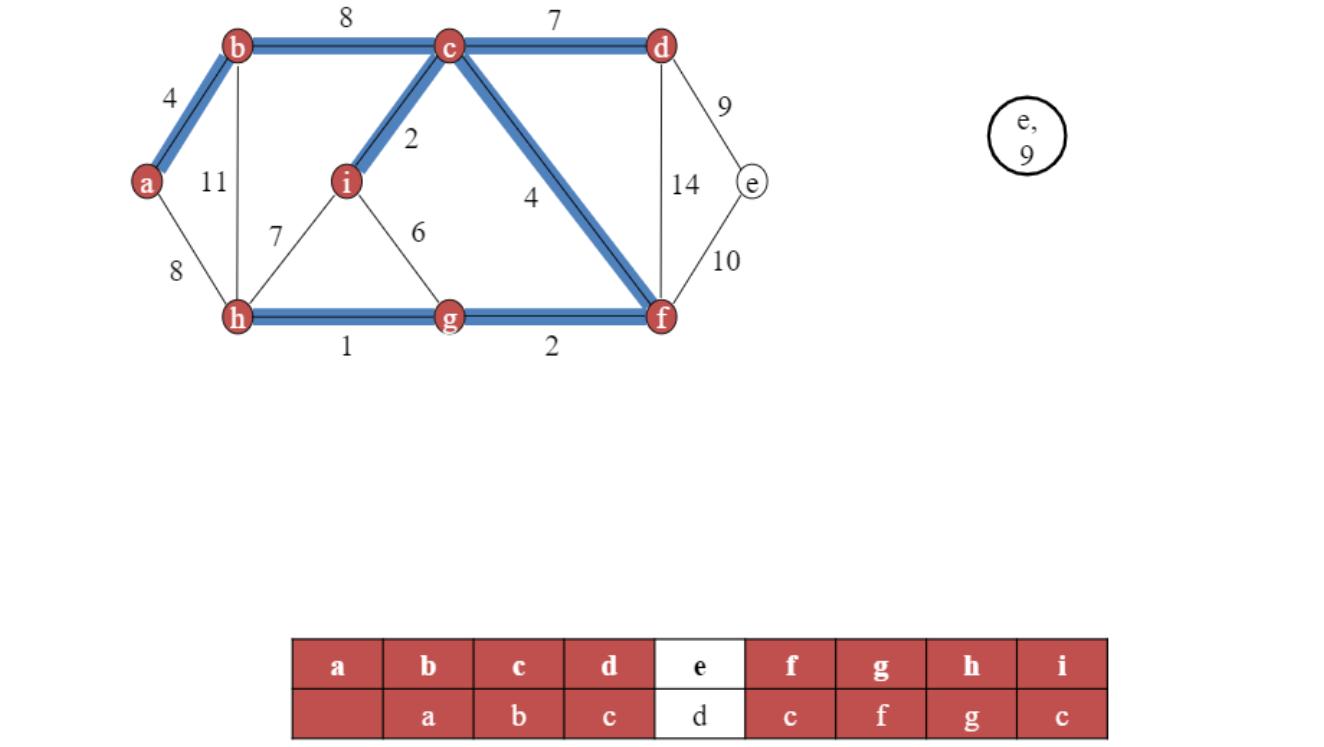
남아있는 노드 없을때 까지 EXTRACT-MIN과 DECREASE-KEY(x,y) 반복

Pseudo Code
MST-PRIM(G, w, r) # line 1
    for each u ∈ G.V
    u.key = ∞ 
    u.π = NIL
    r.key = 0
    Q = G.V
    while Q ≠ Ø # line 6
        u=  EXTRACT-MIN(Q)
        for each v ∈ G.Adj[u]
            if v ∈ Q and w(u, v) < v.key # line 10
                v.π = u
                v.key = w(u, v) # line 12
  • line 1:
    • G : graph
    • w : weight
    • r : 시작 node (랜덤하게 줘도 ok)
  • line 6:
    • Q의 자료구조 : binary min heap
  • line 1~6: BUILD-HEAP
    • 모든 node의 cost (key)를 $\infin$, predecessor를 $NIL$ 로 초기화
    • 시작노드는 cost 0으로 변경
  • line 10~12:
    • UPDATE 하는 경우
    • 아직 heap 남아있고($v ∈ Q$),
      cost 적은 경우($w(u, v) < v.key$)
    • line 11은 predecessor 변경
    • line 12는 decrease key
Time Complexity
  • build heap line2~5
    $O(n)$
  • extract-min : line8
    $O(lgn)$
    그리고 최악의 경우 node 개수인 n회 호출 -> $n\cdot O(lgn)$
  • decrease key : line11~12
    $O(lgn)$
    최악의경우 edge수 만큼.
    -> $O(e\cdot lgn)$

$\therefore O((\vert V\vert +\vert E\vert ) \cdot lg\vert V\vert )$

edge 수 항상 더 많기 때문에
$O(|E|\cdot lg|V|)$

Minimum Spanning Trees

위 알고리즘을 일반화 하기위해 알아둬야 할 몇가지 개념들

14

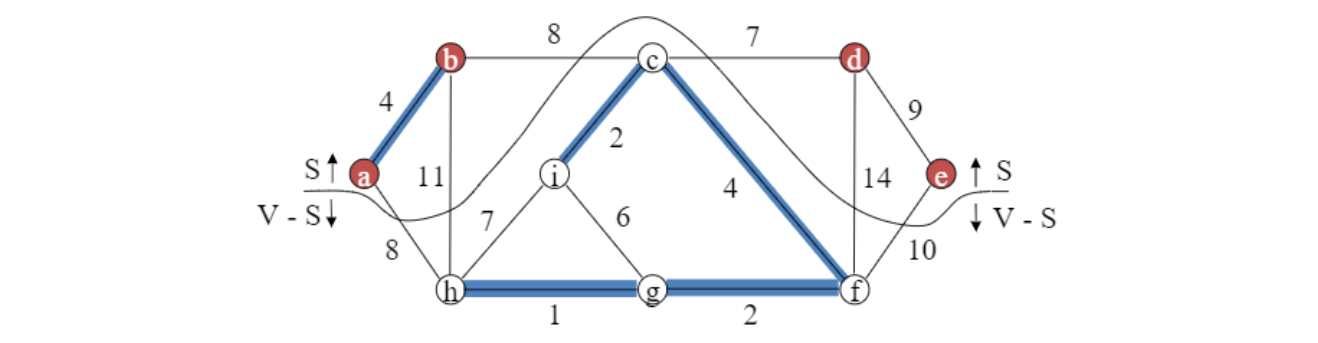
  • Cut :
    • node의 집합 둘로 가르는 것
    • Undirected group $G=(V,E)$의 cut $(S,V-S)$은 $V$의 partition
    • S와 V-S는 서로 여집합 관계
  • Cross :
    • edge가 cut을 cross한다
      = 어떤 edge의 양끝이 다른 partition에 있어서 cut을 cross 하는 경우 = edge의 양끝이 반대편에 있는 상황
    • 한 edge $(u,v)$의 endpoint 하나는 $S$에, 하나는 $V-S$에 있는 경우

      위 예시에서는 $(b,h) \in E$등이 cut $(S,V)$를 cross 함

  • Respect :
    • set A의 edge들 중 어느것도 cut을 cross하지 않는 경우, respect 하다고 함
  • Light edge :
    • cut을 cross하는 edge중 cost가 가장 작은 것

      위 예시에서는 $(c,d)$

📌Theorem 23.1 (#87)
: 하나의 minimum spanning tree만드는 것

1) MST의 일부(subset)인 A가 있을 때,
2) A에 respect 하게 cut 만들고,
3) 이 cut에 대해 cross하는 edge를 찾으면 safe 하기에 이 또한 MST의 subset이다

결론: (어떤 cut이 있을 때) light edge는 safe하다

prim의 알고리즘도 마찬가지임. 특수한 경우. 노드 1개에서 시작해 그것과 나머지 간에 파티션 나눠서 light edge 선택.
그리고 선택한것들과 나머지를 다시.

Outline of the proof

  • Minimum spanning tree $T$가 $A$를 포함한다면,
    (이때 $T$는 light edge $(u,v)$를 포함하지 않는다고 가정)
  • $A\cup {(u,v)}$을 포함하는 또다른 minimum spanning tree $T’$을 만들 수 있음

15

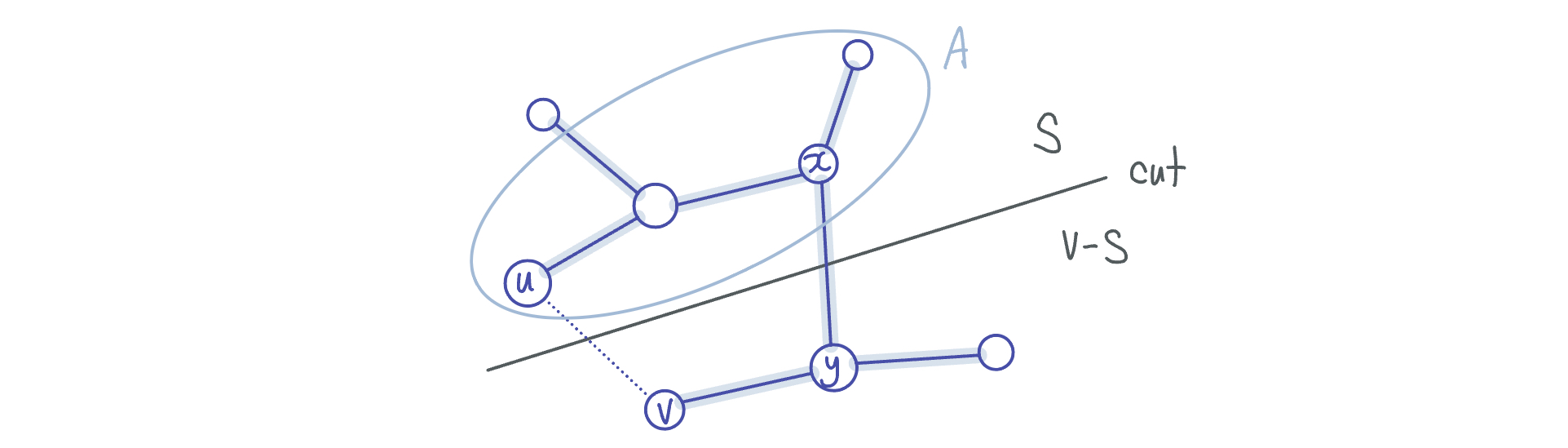
  • edge $(u,v)$는 $T$에 있는 path와 cycle을 형성한다.
    (cut을 지나는 edge는 (x,y)가 유일하기에)

  • u와 v는 cut $(S,V-S)$에 대해 반대 부분에 있기때문에,
    • $T$의 path $p$에는 cut을 cross 하는 최소 한개의 edge가 있다
    • 그리고 그런 edge를 $(x,y)$라 하자

  • cut은 A에 대해 respect 하기 때문에 edge $(x,y)$는 $A$에 포함되지 않는다.

  • edge $(x,y)$는 $T$에서 $u$부분과 $v$를 잇는 unique한 path이기에 edge$(x,y)$를 제거하는 것은 $T$를 두 부분으로 나눔.

  • edge $(u,v)$를 추가하는 것은 새로운 spanning tree를 형성하도록 두 부분을 연결함
    $T’=T-{(x,y)}\cup {(u,v)}$

📌 $T’$이 minimum spanning tree 임을 증명

edge $(u,v)$가 ($(S,V-S)$를 cross 하는) light edge이고, $(x,y)$또한 이 cut을 지나기에

$w(u,v)\leq w(x,y)$

$w(T’)=w(T)-w(x,y)+w(u,v)$
            $\leq w(T)$

하지만 $T$가 Minimum spanning tree이고 $w(T’)\leq w(T)$이기 때문에 $T’$또한 Minimum spanning tree이다.

$(x,y)$보다 $(u,v)$가 cost 적다면
$T’$이 $T$보다 cost적음 ✏️

📌 $(u,v)$가 실제로 $A$에 대한 safe edge임을 증명

$A\subseteq T$ and $(x,y)\notin A \Rarr A \subseteq T’$

$A\subseteq T$인데 A에 포함 안된 $(x,y)$와 $(u,v)$ 를 바꿔치기한게 $T’$이므로 $A \subseteq T’$ ✏️

또한 $T’$이 Minumum spanning tree이므로 $(u,v)$는 A에게 safe.

$(x,y)$ 날리고 $(u,v)$ 연결하면 connectivity 다시 O
$\rarr$ Spanning tree ✏️

📌 Corollary 23.2

  • Let $G=(V,E)$ be a graph
  • Let $A$ be a subset of $E$ that is included in some minimum spanning tree for $G$
  • Let $C=(V_C,E_C)$ be a connected component (tree) in the forest $G_A=(V,A)$
  • If $(u,v)$ is a light edge connecting $C$ to some other component in $G_A$, then $(u,v)$ is safe for $A$

A를 그래프 G의 minimum spanning tree의 subset이라고 할 때

$(u,v)$가 A와 다른 component를 잇는 light edge라고 할 때 $(u,v)$는 A에 safe

Connected components :
연결되어있는것들의 덩어리
예를 들어,
0-0-0       0-0       0-0-0       0
이렇다면 connected component는 4개

Proof

Minimum Spanning Tree

A에 respect 한 cut $(V_C,V-V_C)$이 있고, $(u,v)$가 이 cut에 대한 light edge이다.
이 경우 $(u,v)$는 A에 대해 safe

theorem이 성립하기에 이것 또한 성립

Prim’s Algorithm

$\subset$ generic MST

  • set A의 edge들은 항상 single tree를 형성함
  • Tree는 arbitary root vertex $r$부터 시작해서 $V$의 모든 vertex에 span할 때 까지 grow

    처음 노드 1개, empty set

  • 각 단계마다 $G_A=(V,A)$의 고립된 vertex와 $A$를 연결하는 light edge들은 tree $A$에 추가된다.

    A와 나머지 partition 후 light edge 선택

  • Corollary 23.2에 의해, 이 규칙은 $A$에 safe 한 edge들만 추가한다.
  • 따라서 알고리즘이 실행되면, $A$의 edge들은 Minimum spanning tree를 형성한다.

Kruskal’s Algorithm

  • Growing forest에 추가하기위해 forest의 어떤 두 tree를 연결하는 safe edge이며 least weight인 $(u,v)$를 찾는다.

  • $C_1$과 $C_2$가 $(u,v)$에 의해 연결되는 두 tree를 의미 할 때

  • $(u,v)$가 $C_1$과 다른 tree를 연결하는 light edge이기에, Corollary 23.2는 $(u,v)$가 $C_1$에 대해 safe edge임을 나타낸다.

Kruskal’s Algorithm

동작방식

  • 전체 edge sort 후 edge의 weight 제일 작은 것 반복적으로 선택. (이 때 edge의 선댁으로 cycle이 되지 않는 조건만 만족하면서)

이 때 자료구조 : disjoint set
$\rarr$ 같은 connected component 찾는 일 함

Pseudo code

MST-KRUSKAL(G, w)
    A = Ø
    for each vertex v ∈ G.V
        MAKE-SET(v)
    sort the edges of G.E into nondecreasing order by weight w
    for each edge (u, v) ∈ G.E, taken in nondecreasing order by weight
        if FIND-SET(u) ≠ FIND-SET(v)
            A = A ∪{(u, v)}
            UNION(u, v)
    return  A

출처 : 2023-2 ITE2039 수업