Contents

  • Definition
  • Dijkstra’s algorithm
  • The Bellman-Ford algorithm
  • Single-sorce shortest paths in directed acrylic graphs

Single-Source Shortest Path

✏️ 이전 Minimum Spanning Tree에서는 모든 노드를 연결하는 최소 cost인 tree 찾는것이 목표였음.

이번 post에서는 전체 tree가 아닌 path 찾는것이 목표.

Definition

사용하는 개념들 정리

Edge weight

: 특정 edge의 가중치

Path weight

: Path에 있는 모든 edge weight들의 합

Shortest path

u에서 v로 가는 path 중 weight가 최소인 것 (이때 u는 source, v는 destination)

Shortest path weight

u에서 v까지 가는 shortest-path의 weight로, $\delta(u,v)$라고 표기

Shortest path problem

Shortest path문제는, source와 destination의 개수에 따라 4종류가 있다

  • Singles-source & Single destination

  • **Single-source (& all destinations)**

  • Single-destination (& all sources)

  • All pairs

single source (& all destinaton) 문제로 다른 모든 문제 풀 수 있기에

Negative-weight edges

생각해볼 point
모든 negative-weight edge들이 문제를 유발하는가?
모든 negative-weight cycle이 문제를 유발하는가?
모든 reachable negative cycle이 문제를 유발하는가?

$\Rarr$ source에서 reachable 한 negative-weight cycle이 없을 때 single-source shortest path가 정의 될 수 있다

Cycle

shortest path는 cycle을 포함하지 않으므로,
$\therefore$ shortest path는 최대 $|V|-1$

Predecessor subgraph

모든 SSSSP들을 compact하게 저장하는 shortest path tree

optimal substructure

푸는과정에서 shortest path 기록하며 update,
최종적으로 predecessor subgraph

Relaxation

RELAX(u, v, w)
    if d[v] > d[u] + w[u, v]
        then d[v] ← d[u] + w[u, v]
            π[v]← u

Dijkstra’s algorithm

모든 weight nonnegative일때 정상작동

동작방식
1) 해당 노드로부터 갈 수 있는 노드들의 cost 갱신 (다이나믹 프로그래밍) 2) 방문 안한 노드 중 가장 cost 작은 노드 선택 (Greedy 알고리즘) 3) 1,2 반복

5

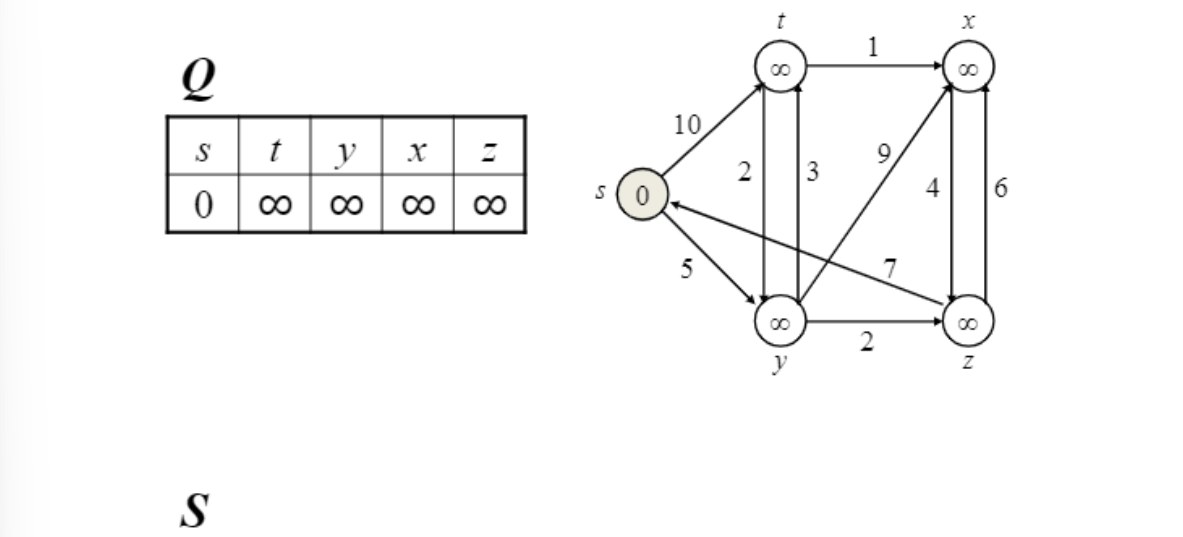
초기화

6

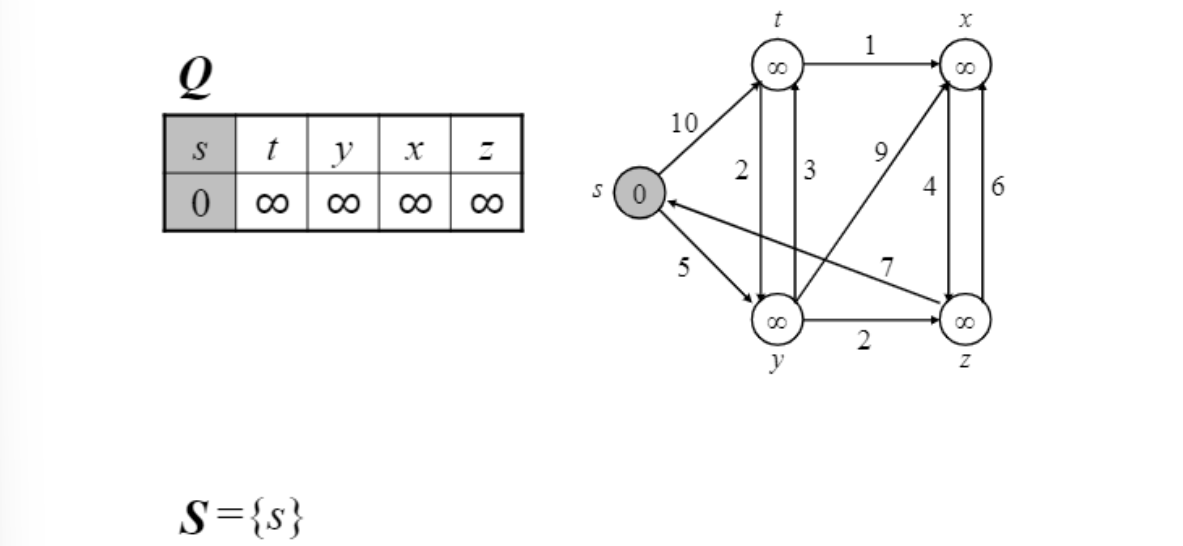
최소인 source node $s$선택

7

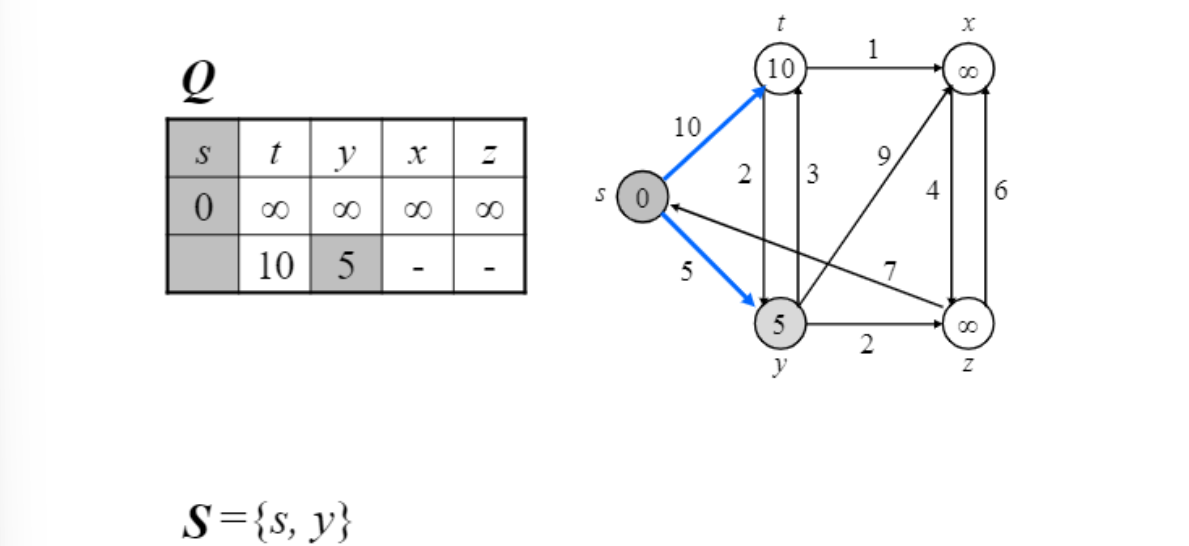
$s$와 adjacent 한 vertex 값들 update 후 그 중 최소인 $y$선택

8

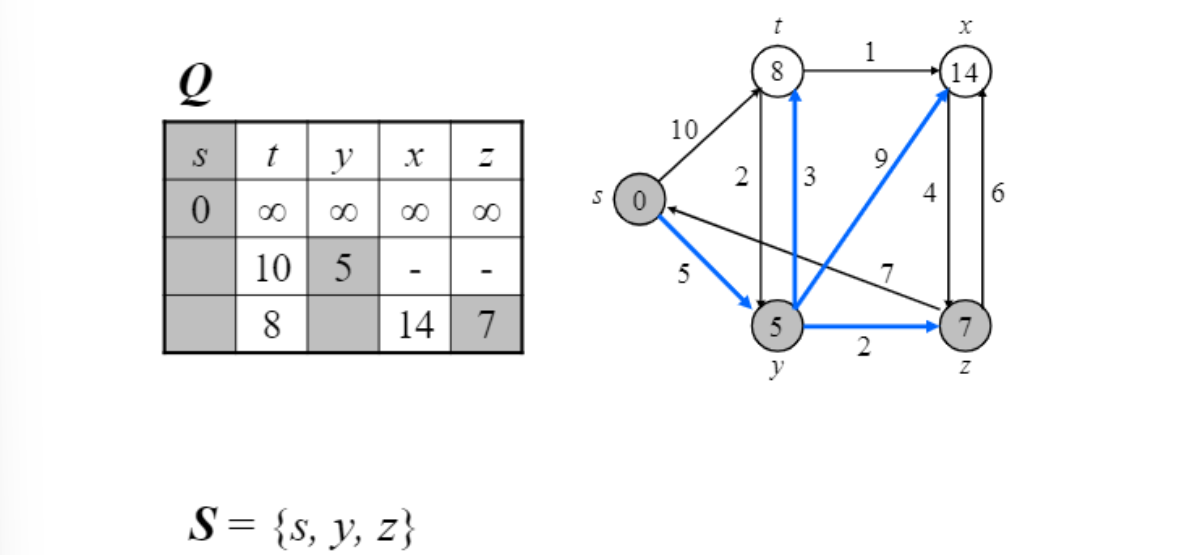
$y$와 adjacent 한 vertex 값들 update 후 그 중 최소인 $z$선택

…

9

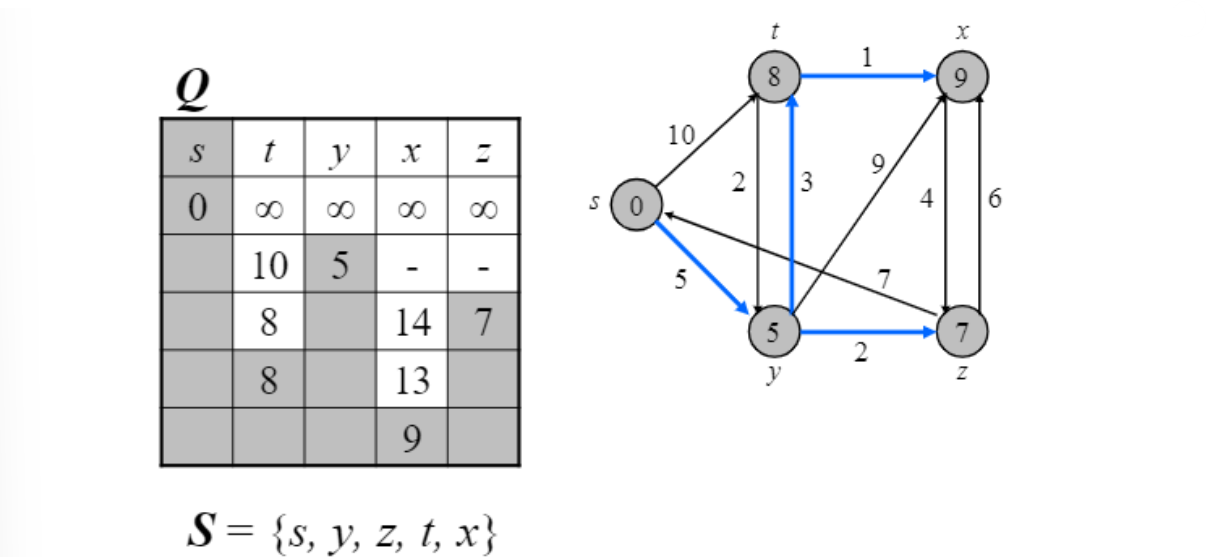
남은 노드 없을 때까지 위의 과정 반복



heap 쓰는 경우도 마찬가지 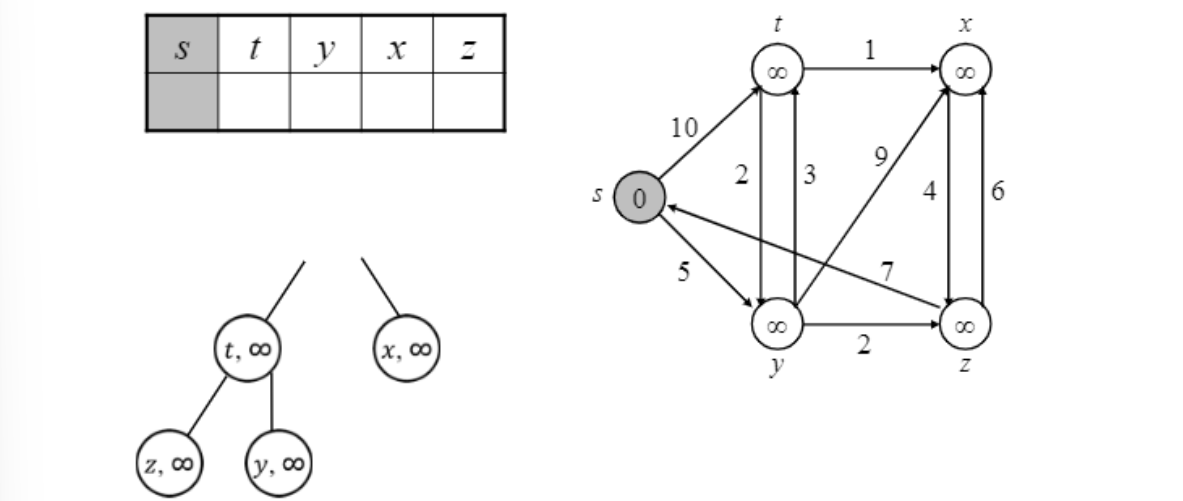10 초기화 후 extract min, min-heapify …


Pseudo code

DIJKSTRA(G, w, s)
    INITIALIZE-SINGLE-SOURCE(G, s)  // 첫노드 0, 나머지 ∞
    S = Ø   // empty set
    Q = G.V
    while Q ≠ Ø
        u = EXTRACT-MIN(Q)  // S 시작 노드 1개에서 시작해서, 
                            // Q에 남아있는 것 중 d값 제일 작은 것 
        S = S ∪ {u}
        for each vertex v ∈ G.Adj[u]
            RELAX(u, v, w)

Negative-weight 없다는 가정하에 동작
이런 제한 있음에도 실제 application 또한 negative 많지 않기에 유용

shortest path가 알려진 것들의 집합 S, shortest path 모르는 것들은 V-S에.
Dijkstra의 목표는 모두 S에 넣는 것.

Running time

while loop 이전까지 $\rarr |V|$

while loop 내부는
EXTRACT-MIN(Q) : $O(|V| \cdot lg|V|)$
RELAX(u,v,w) : $O(|E|\cdot lg|V|)$

  • (unsorted) array 사용한 경우, $O(V^2)$

    매번 제일 작은 것 찾는 시간이 n에 비례.
    $\therefore n^2$

  • heap 사용하면, $O(VlgV+ElgV)$

증명에 사용할 definition

  • u에서 v까지 distance
    = $\delta (u,v)$ = 최단 거리
Problem

NONNegative인 edge weight를 가진 Directed graph $G(V,E)$와
Special source vertex $s \in V$ 가 주어졌을 때,
Source vertex에서 $G$의 모든 vertex까지 distance를 구하라

  • $d[v]$ : estimates the shortest path = 지금까지 추정하는 최단거리
  • $\pi[v]$ : predecessor pointer of the path = u에서 v까지 가는 path인 경우 v 바로 앞 노드(=predecessor)
Principle observation
  • Short path의 모든 subpath 또한 항상 shortest path여야한다.

    각 vertex에 대한 shortest path의 추정을 $d[v]$에 저장(유지)해둔다

  • 초기에는, $d[s]=0$, $d[v]=\infin$
  • $d[v]\geq \delta(s,v)$ : 알고리즘이 진행되면서 $d[v]$가 $\delta(s,v)$에 수렴할 때 까지 update 진행
    (이 process를 relaxation이라고 한다. = relaxation 통해 $d[v]$ 업데이트)
if(d[u]+ w[u, v]< d[v])
    d[v]= d[u]+ w[u, v];
    π[v]= u;

📌 Dijkstra가 DP인 이유
최단거리는 여러개의 최단거리의 합으로 이루어져있기에,
이전까지 구한 최단거리를 기록해두고 이를 사용

진행

  • vertex들의 subset $S ( \subseteq V)$ 를, shortest distance를 ‘안다’고 주장하는, $d[v] = \delta(s,v)$로 유지
    = $d[v] = \delta(s,v)$인 것들을 $S$에 넣어줌

  • 초기에 $S={ }$. 그리고 각 stage 마다 하나씩 vertex들을 $V-S$에서 선택함

  • $d[u]$가 최소인 vertex를 선택. 그리고 이를 모든 operation(Insert, Delete_min, Decrease_key)이 $O(lgn)$시간에 수행 될 수 있도록 priority queue로 구현

  • 각 stage 마다

    • unknown vertex 중 최소의 $d[v]$값을 가지는 vertex $u$ 선택
    • $s$에서 $u$로 가는 shortest path는 안다고(known) 정의
    • update $d[v]$ : $d[v]$가 개선되었다면 $d[v]=d[v]+w[u,v]$로 update
      ($v$로 가는 path에 $u$를 사용하는 것이 좋은 아이디어인지 결정)

증명

Lemma (보조정리)

vertex $u$가 $S$에 추가되었을 때, $d[u]=\delta (s,u)$

Proof 📌

증명하고자 하는건,
“Node $u$의 $d$값이 제일 작아 (extract-min 통해서)선택되면, $u$의 $d$값은 실제 $\delta$(delta)이다”

“Proof by contradiction” 사용

(모든 weight가 STRICTLY positive라고 가정)

vertex $u$가 $S$에 추가되었지만 $d[u]\neq \delta(s,u)$라면,
$d[u]> \delta(s,u)$ ($\because$ $d$는 $\delta$보다 크거나 같다는 정의)

$u$를 추가하기 직전 상황을 검토해 보면,

$s$에서 $u$까지 실제 최단거리를 $s\rarr x\rarr y\rarr u $ $(x\in S, y\in V-S)$라고 하면,

$d[u]\neq \delta(s,u)$라고 했기에 최단거리는 따로 있는 것.

그리고 $s$에서 $u$까지 path의 중간에 $y$가 있고, 모든 edge는 positive여서 $\delta (s,y)<\delta (s,u)$성립

$s\rarr x\rarr y\rarr u $가 최단경로라 가정했기에,
$d[y]=\delta(s,y)<\delta(s,u)<d[u]$

$\therefore u$ 이전에 $y$가 추가되었어야 함. $\rarr$ contradiction to our assumption

📌 $y=u$일 수 없는가? $\rarr$ NO!
$\because d[u] = \delta(s,u)$ 이고, 우리는 $x$를 추가하기 전에 relaxation 을 적용했기 때문

❗ Prim VS Dijkstra
동작 아이디어가 유사해서 헷갈려서 정리해 본 두 알고리즘의 공통점과 차이점

<공통점>
집합 S에 매 step마다 최소인것을 하나씩 추가

<목표 차이>
Prim : Minimum Spanning Tree
= 모든 node연결이 목표
-> 집합 S과의 최소 distance인 node 찾음

Dijkstra : Shortesst Path
= 두 node 잇는 shortest path 찾는 것이 목표
-> 집합 S의 시작 node와의 최소 distance 찾음

위와 같이 두 알고리즘의 목표가 다르다는 차이 뿐 아니라 

<동작 조건 차이>
Prim은 undirected 에서만 동작, Dijkstra는 무관
Prim은 negative weight 가능, Dijkstra는 negative 불가능

(Prim은 Undirected weighted graph에서)
(Dijkstra는 nonnegative weight의 graph에서)

<공통점에서 이야기하는 '최소'의 차이>
Prim : 집합 S와 닿아있는 모든 edge 중 최소인 것
Dijkstra : V-S인 node중 시작 node로부터 distance가 최소인 것

Bellman-Ford algorithm

: single source shortest-path problem을 negative weight도 포함하는 general case에 대해 푼다.

BELLMAN-FORD(G, w, s)
    INITIALIZE-SINGLE-SOURCE(G, s)
    for i= 1 to |G.V| -1 // 모든 shortest path의 길이 구하는 loop
        for each edge(u, v) ∈ G.E // n-1번째 node까지 순차적으로 RELAX
            RELAX(u, v, w)
    for each edge(u, v) ∈ G.E // negative weight cycle 있는지 검사하는 loop
        if v.d > u.d + w(u, v) // negative cycle이 있다는 뜻
            return FALSE
    return TRUE

모든 shortest path의 길이 구하는 부분에서 n-1인 이유
n-1 : 모든 node.
$\therefore$ n-1보다 크면 중복 발생한다는 것
= cycle 有

Relaxation order

모든 edge 일렬로 나열.
relaxation 순서는 중요하지 X
$\because$ 어차피 매번 전부 할꺼임

Running time

: $O(VE)$

pseudo code Initialize 직후 세 줄 부분

  • 첫번째 for loop -> $V$
    Negative cycle이 없기 때문에, $\vert V\vert -1$ 회의 반복 이후
    $d[v]=\delta(s,v)$
    최대 (노드의 개수-1)만큼 반복이기 때문
  • 두번째 for loop -> $E$
    매번 edge 개수만큼 RELAX하므로

증명

📌 “Negative cycle이 있을 때 False를 return한다” 증명

$v_0=v_k$인 $<v_0, v_1,…,v_k>$라는 negative cycle이 있지만 Bellman-Ford가 True를 return 한다고 가정하자.

negative cycle -> False 증명 위해
negative cycle -> True라고 가정.
이후 모순인 부분 보이기.

True를 return 하기에,
모든 $i-1,2,..,k$ 에 대해 $d[v_i]\leq d[v_{i-1}]+w[v_{i-1},v_i]$ 성립한다

negative cycle이 있다면, Relaxation 한번 더 진행한 결과 distance인 우측항이 더 작아서 (>) False를 return 하는 알고리즘이지만,
지금은 negative cycle이 있음에도 좌측항이 작거나같다는 ($\leq$) True return 하는 가정

$\sum_{i=1}^k d[v_i]\leq \sum_{i=1}^k(d[v_{i-1}]+w[v_{i-1},v_i])$
                    $=\sum_{i=1}^k d[v_{i-1}]+\sum_{i=1}^kw[v_{i-1},v_i]$

cycle이기에 $v_0, v_k$가 같으므로
$\sum_{i=1}^k d[v_i] = \sum_{i=1}^kd[v_{i-1}]$

따라서 $0\leq 0+\sum_{i=1}^kw[v_{i-1},v_i]$

하지만 $\sum_{i=1}^kw[v_{i-1},v_i]$는
$w[v_0,v_1]…[v_{i-1},v-i]=<v_0,v_1,..v_k>$
즉 negative cycle의 sum과 동일하기 때문에 음수.

=> Contradiction

❗ Dijkstra VS Bellman-Ford
동작 목표가 동일해서 헷갈려서 정리한 공통점과 차이점

<공통점>
SSSP(Single Source Shortest Path) 문제

<동작 조건 차이>
Dijkstra : negative weight 불가
Bellman-Ford : negative weight 가능

<동작 방식 차이>
Dijkstra : 시작 node와 "닿아있는 edge들로 확장해가며" node까지 distance update
Bellman-Ford : "매 step마다 모든 edge기준" node 까지 distance update

SSSP in directed acyclic graphs(DAG)

cycle이 없다는 특수 case에서 SSSP(Single source shortest path)

✏️ Topological sort?
topological sort 하려면 cycle 없어야함. (direct acyclic)
topological sort 간단히 하려면 DFS
출력 순서: finish time의 역순. 
out degree 없는 것

Pseudo code

DAG-SHORTEST-PATHS(G, w, s)
1   topologically sort the vertices of G
2   INITIALIZE-SINGLE-SOURCE(G, s) // DFS 하는시간: |V|+|E|
3   for each vertex u, taken in topologically sorted order
4       for each vertex v∈G.Adj[u]
5           RELAX(u, v, w) // edge 개수만큼 반복

topological sort로 node 순서 정하고,
adjacent 한지 보는 것.
$\therefore$ 앞에서 본것들 보다 빠름

동작 방식

“Topological sort 했으면 edge들만 다 보면 된다!”

Source node 여서 $s=0$으로 시작

1 2 3 4

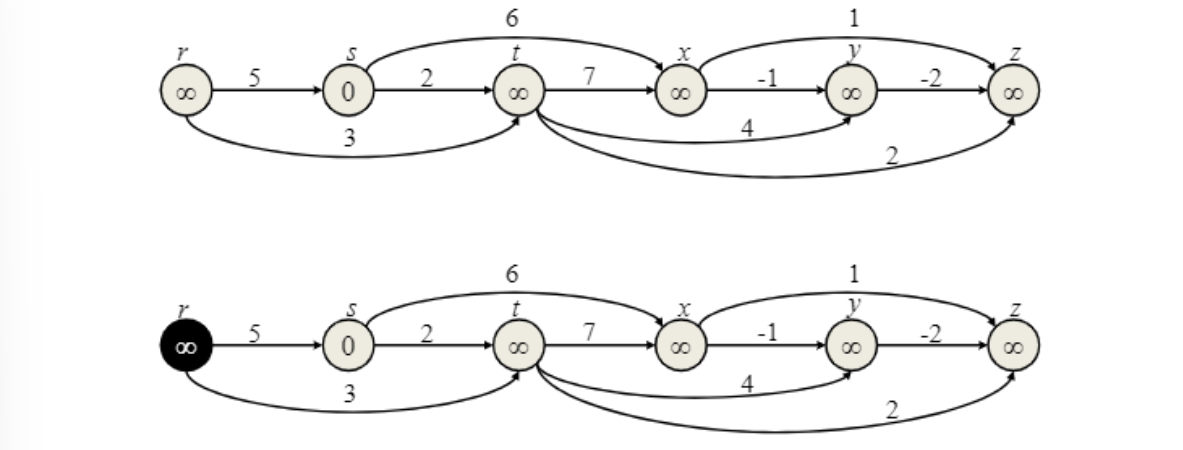
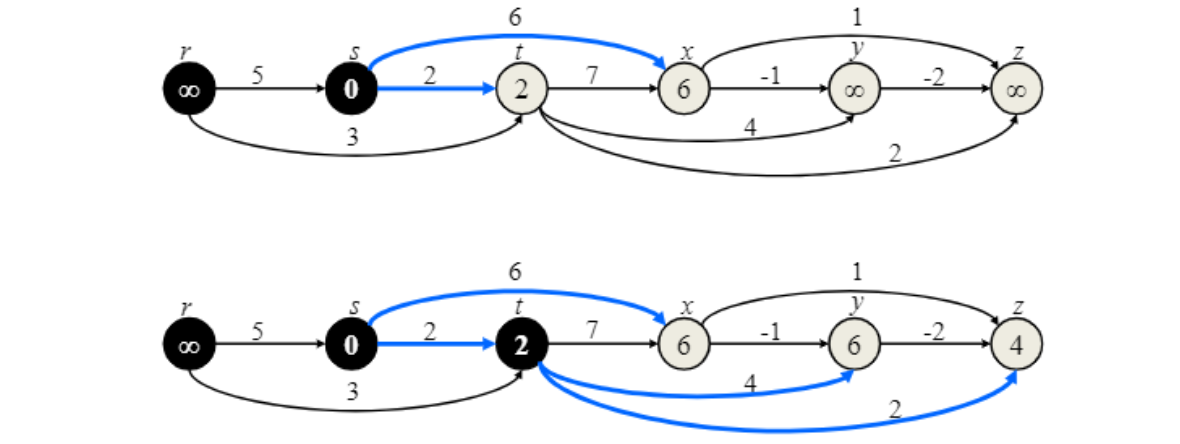
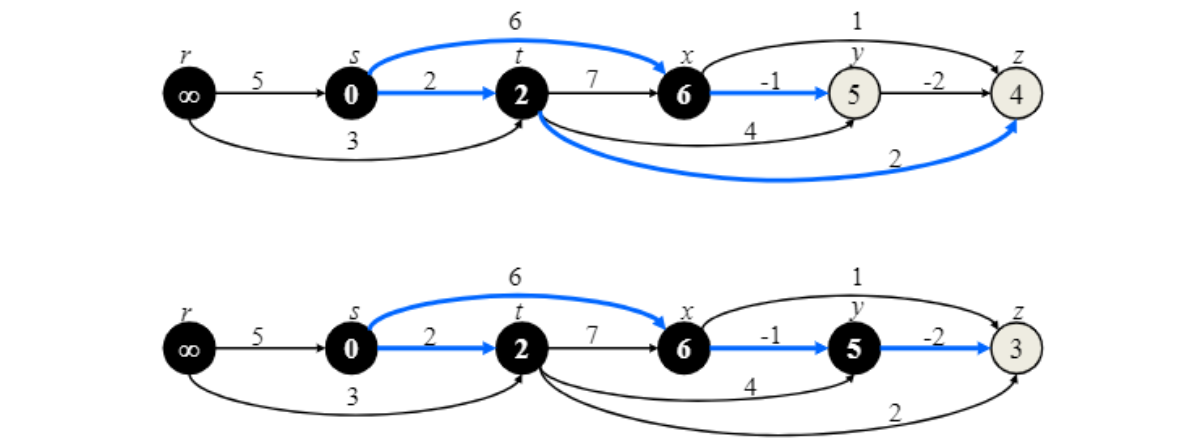
Running time

: $O(V+E)$

응용 application: PERT chart

개념
  • PERT : Program Evaluation and Review Technique
  • 경영학, 업무관리에서 사용
  • 각각의 edge가 task, job을 나타내고
  • edge weight는 각 job들을 수행하는데 걸리는 시간을 의미.
  • DAG를 통과하는 path는 특정 순서를 지켜야하는 job들의 sequence를 의미

    $u$ -> $v$ -> $x$라면 이것이 일이 지켜야하는 순서

  • “Critical path”란, DAG에서 longest path 의미.
    • shortest path를 알아보았던 이전 알고리즘들과 달리, weight가 가장 높은 경로에 관심.

      $\because $ 순서관계 지키면서 가장 오래 걸리는 시간 구하고, 이걸 통해 “최대 @시간 걸리겠다” 등을 얻고자 함 (어디에 집중적으로 자원 투자할지 등)

방법

“Edge weight를 전부 negative로 바꾸고, DAG-shortest-path 수행!”

출처 : 2023-2 ITE2039 수업