Data Structures for Disjoint Sets

Contents

• Disjoint-sets
• Disjoint-set operations
• An application of disjoint-set data structures
• Disjoint-set data structures

---

Disjoint-sets

: 교집합이 없으면 “disjoint” 하다고 함

• 두 set A와 B가 disjoint 하다 = 두 set의 교집합이 없다

  Ex. $ A = {1,2}, B={3,4}$

• Set들 $S_1, S_2,…,S_k$가 disjoint 하다 = 모든 두 set $S_i, S_j$가 disjoint.

Ex. $ S_1 = {1,2,3}, S_2={4,8}, S_3={5,7}$

• Collection of disjoint sets
  = set of disjoint sets

Ex. $ {{1,2,3}, {4,8},{5,7}}$

• collection의 각 set은 **representative member**를 가지고, 각 set은 그 member에 의해 identify됨

Ex. $ {{1,2,3}, {4,8},{5,7}}$
1,4,7

• A collection of dynamic disjoint sets
  • Dynamic = set이 변화한다
    • 새 set created

      Ex. ${{1, 2, 3}, {4, 8}, {5,7}} \rarr {{1, 2, 3}, {4, 8}, {5,7}, {9}} $

    • 두 set united

      Ex. ${{1, 2, 3}, {4, 8}, {5,7}} \rarr {{1, 2, 3}, {4, 8, 5,7}} $

Disjoint-set operations

• Operation 종류
  • MAKE-SET(x)
  • UNION(x,y)
  • FIND-SET(x)

• MAKE-SET(x)

  member x가 주어지면, set x 생성

  Ex. MAKE-SET(9)
  ${{1, 2, 3}, {4, 8}, {5,7}} \rarr {{1, 2, 3}, {4, 8}, {5,7}, {9}} $

• UNION(x,y)

  두 member x와 y가 주어진 경우, x를 포함하는 set과 y를 포함하는 set을 합한다.

  Ex. UNION(1,4)
  ${{1, 2, 3}, {4, 8}, {5,7}} \rarr {{1, 2, 3, 4, 8}, { 5,7}} $

• FIND-SET(x)

  x를 포함하는 set의 representative 찾기

  Ex. FIND-SET(5): 7
  ❗주의할 부분 : parameter가 있는 index등 아니고, 그 set의 representative!!

• 문제:
  MAKE-SET(x), UNION(x,y), FIND-SET(x) 과 같은 disjoint-set operation을 지원하는 dynamic disjoint set의 collection 유지하기 위한 자료구조 개발 하는 것

• running time을 위한 parameter 분석
  • #Total operations : m
  • #MAKE-SET ops : n
  • #UNION ops : u
  • #FIND-SET ops : f
  • m = n+ u + f
• $u\leq n-1$
  • n은 MAKE-SET operation에 의해 생성된 숫자 set의 개수
  • 각 UNION은 set의 개수를 하나 줄임
  • n-1회의 UNION 후 우리는 1개의 set만 남았고 더이상 UNION할 수 없음
• 이 때 assumption : 처음 n개의 operation은 MAKE-SEToperation

An application of disjoint-set data structures

• Computing connected comdponents (CC)

  • static graph

  • dynamic graph

CONNECTED-COMPONENTS(G)
    for each vertex v∈G.V
        MAKE-SET(v)
    for each edge (u, v) ∈ G.E
        if FIND-SET(u) ≠ FIND-SET(v)
            UNION(u, v)

SAME-COMPONENT(u, v)
    if  FIND-SET(u) == FIND-SET(v)
        return TRUE
    else return FALSE

(SKIP)

#20~

Disjoint-set data structures

• linked-list representation
• forest representation

linked-list representation

• 각 set은 linked list로 표현됨
• disjoint set의 member는 linked list의 object
• linked list의 첫 object는 representative ⭐

• 모든 object는 representative로 pointer 가지고 있다. ⭐

• 예제 ${{b, c, e, h}, { d,f,g}} $ set을 linked list로 표현하면,
  2개의 linked list가 필요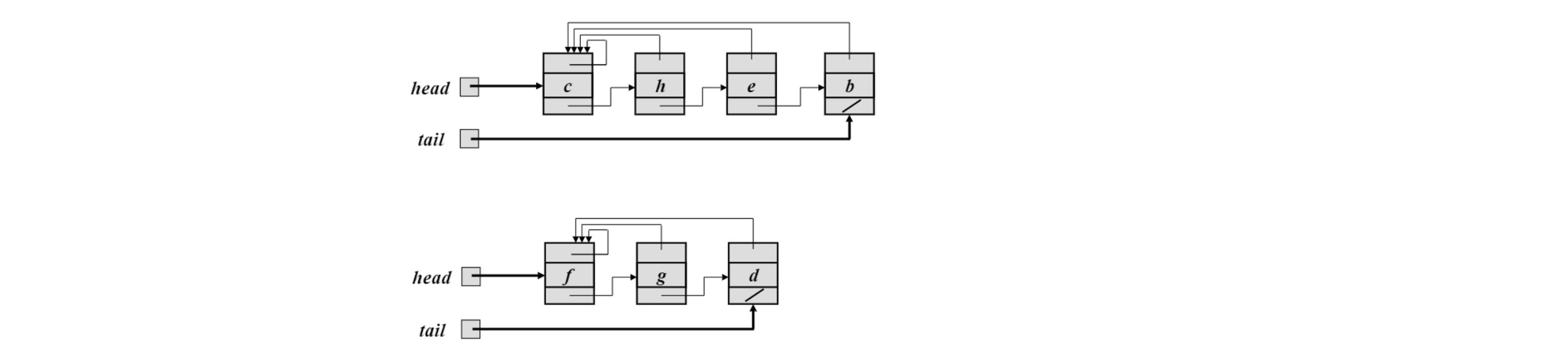

• MAKE-SET(x) : $\theta(1)$

• FIND-SET(x) : $\theta(1)$

• UNION(x,y) : 한 link를 다른 link에 attatch 하는 것
  • tail pointer 수정 & 두 linked list 연결 : $\theta(1)$
  • 뒤에 붙는 링크의 모든 pointer를 representative로 수정 : $\theta(m_2)$
    이 때 $m_2$는 뒤에 붙는 list의 object #
    $\therefore$ (뒤의 list의 pointer를 다 수정해 주어야 하니) 짧은link를 뒤에 붙인다

$m$개의 operation에 대한 Running time

: $m=n+f+u$ (각각이 MAKE-SET(x), FIND-SET(x), UNION(x,y))

FIND-SET(x)은 representation 따라가면 되어서 constant시간동안 가능. MAKE-SET(x)도 마찬가지.

UNION(x,y)은 최악의 경우, make-set해둔 원소 개수를 upper bound로 가지는 횟수만큼 update 해야함.
최악의 update 횟수= $n$ -> 그리고 이게 $u$번 발생
$n\times u$이고, $u\leq n-1$이기 때문에 $\theta(n^2)$

• Simple implementation
  $O(n+f+n^2)$ 이고, $u<n$ 이기 때문에
  $O(m+n^2)$

• A weighted-union heuristic

  두 linked list를 union 하는 경우, 짧은것을 뒤에 붙이는 것을 말함

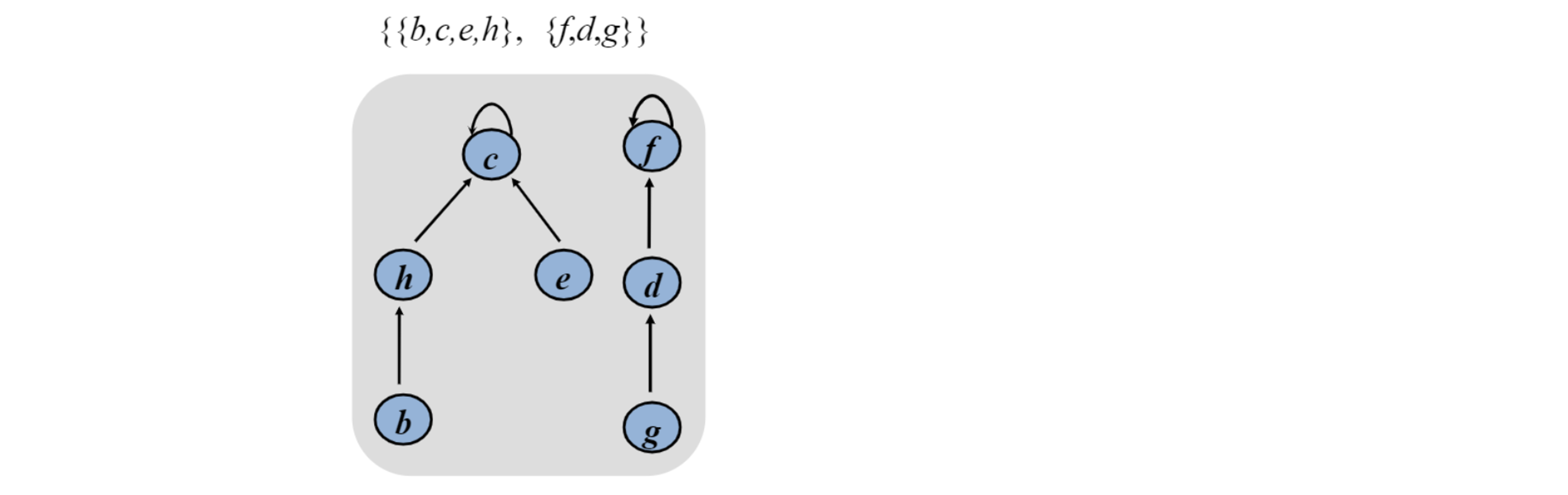
Forest representation

• 각 set은 tree로 표현됨
• 각 member는 parent에 대한 pointer만 가지고 있음
• 각 tree의 root는 representative.

MAKE-SET(x) 
    x. p= x

FIND-SET(x)
    if  x == x.p
        return x
    else return FIND-SET(x. p)

Union by rank

: 작은 tree를 higher tree에 붙이기.
각 노드는, 노드 height의 upper bound인 rank를 저장해둠
두 root의 rank를 비교해서 rank가 작은 tree를 attatch

find set -> 각각의 depth가 얼마나 깊은지에 따라 결정되기 때문에,
tree 2개도 (linked list와 마찬가지로) 키가 작은 것이 키가 큰것에 붙는게 나음

키 큰지는 어떻게? height 계산하려면 따라내려가는것.
(따라내려가는것 줄여보자고 height 계산하는건데 계산하는데 시간 소요되면 안되니,) height를 root에 저장해두기 = rank

❗ Union by rank 하는데 걸리는 시간 생각해보기!!

MAKE-SET(x)
    x.p= x
    x.rank = 0

UNION(x, y)
    LINK(FIND-SET(x), FIND-SET(y))

LINK(x, y)
    if  x. rank > y. rank
        y. p= x
    else x. p= y
        if  x. rank= = y. rank
            y. rank= y. rank + 1

-> but, union by rank 방식으로는 height가 계속 늘어나기만 함
$\therefore$ FIND-SET오래걸림.

Path compression

: FIND-SET 동안 parent를 root로 변경!

FIND-SET(x)
    if  x ≠ x.p
        x. p= FIND-SET(x. p)
    return x. p

depth가 1이 됨.
어떤 find 하는데 시간이 오래걸리지만 다른것 find 할 때 시간 단축됨.
worst case 따지기 위해서는 amortized analysis 해야함

• worst case running time : $O(m~~\alpha(n))$
  • $m$ : 전체 operation의 개수
    $\alpha(n)$ : 원소의 개수와 관련있는 함수인데, 거의 상수나 다름없는 함수라는 의미

---

출처 : 2023-2 ITE2039 수업