Contents

  • Graphs(part1)
    • Graph basics
    • Graph representation
      • Adjacency-list representation
      • Adjacency-matrix representation
  • Searching a graph (part2)
    • Breadth-first search
    • Depth-first search
  • Applications of depth-first search(part3)
    • Topological sort

Elementary Graph Algorithms 3

Definition

DAG(Directed acyclic graph)에서 전체 vertex들을 linear ordering 하는 것

<1-1. BFS, array 사용>

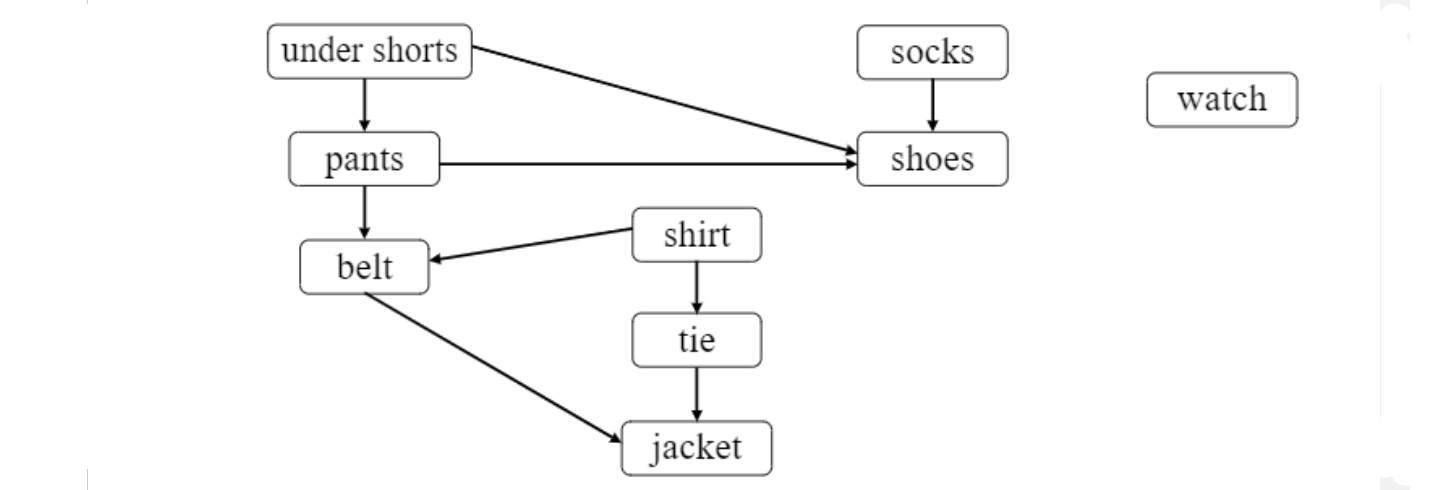1 위와같이 DAG 형태의 그래프가 주어졌을 때,

2 모든 edge의 방향이 좌측에서 우측으로 가도록 sort.

3 이후 Indegree Array를 만들고,

아래의 과정을 반복:
1) indegree가 0인 것들을 하나씩 제거하고, (제거한 node의 indegree array의 값은 -1로)

0인것이 여러개 있는 경우, 책에서는 제일 좌측부터 제거함 2) 그것과 연결된 edge도 지워지며 indegree array값도 update

4
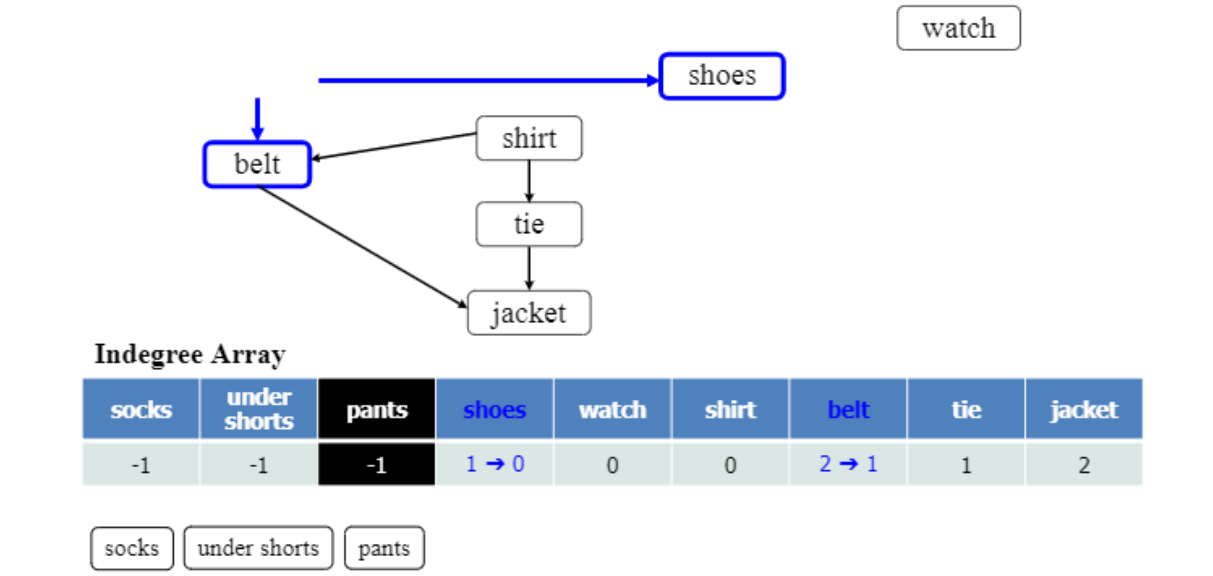
동작 중간 상황 이미지

모든 indegree array의 값이 -1이 되면 종료

Time complexity

$O(V^2)$

<1-2. BFS, stack 사용>

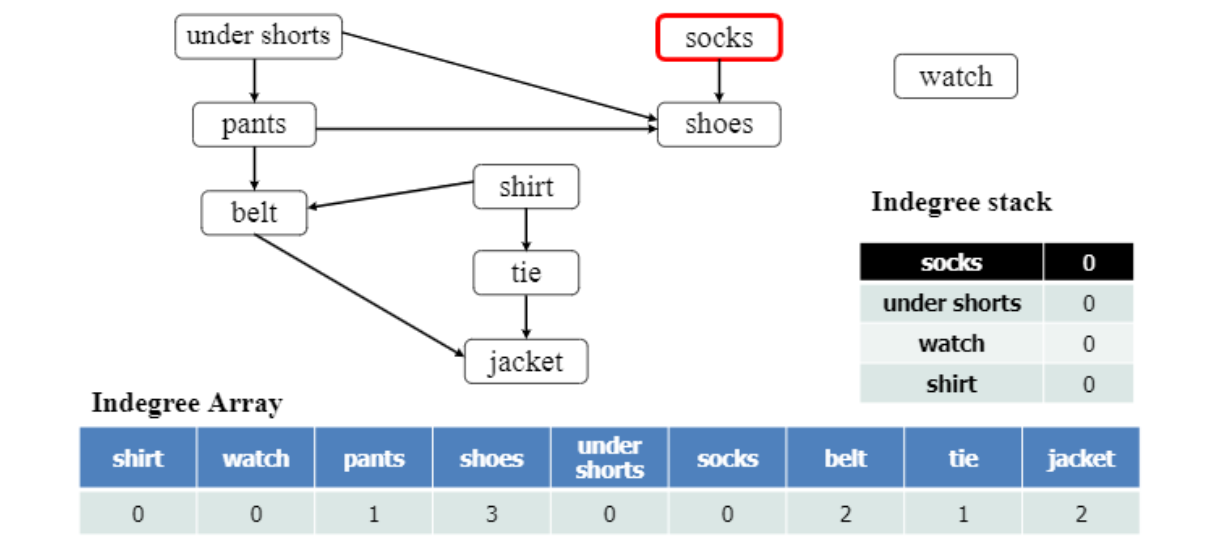6 이런 형태로 초기화 후

7 8
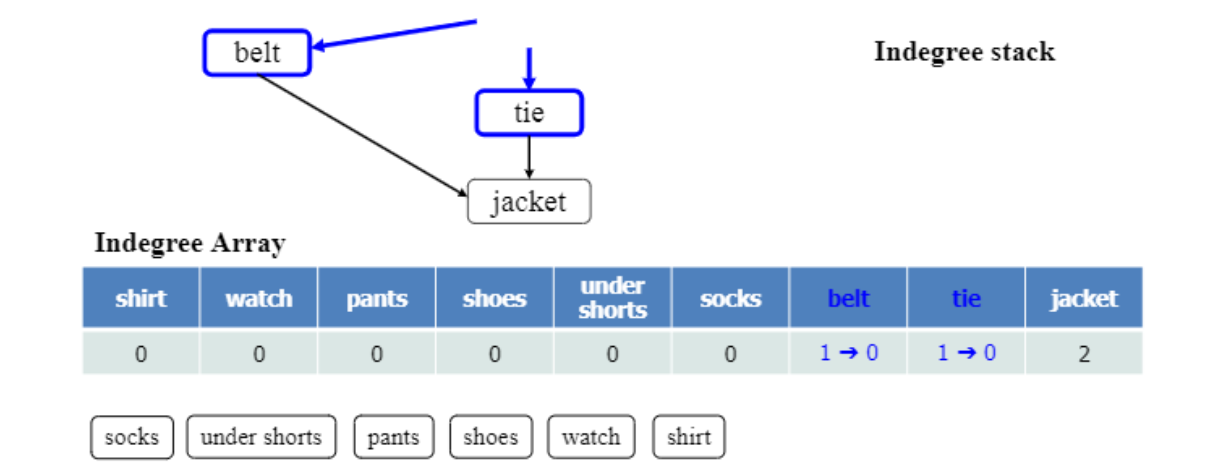
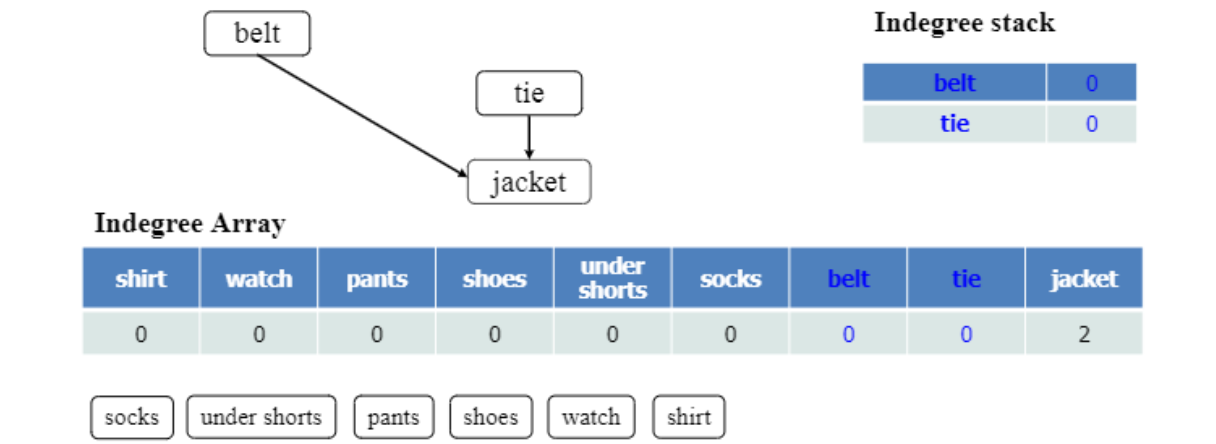
진행 중간 상황) 이런 동일한 방식으로 사용

Time complexity

$O(\vert V\vert +\vert E\vert)$

9

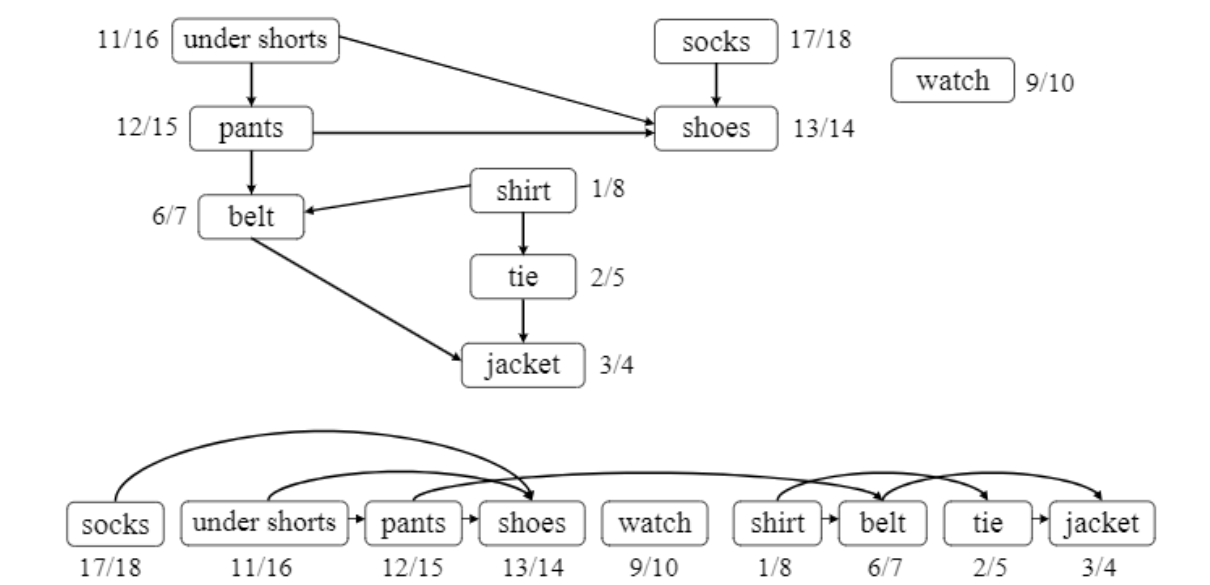
finish time의 역순으로 sort

증명

📌 finish time의 역순이 topological sort인 이유

1(Lemma). G가 acyclic 하다면 dfs한 G는 back edge가 없다. 
2(Theorem). u에서 v로 가는 edge가 있다면, v.f < u.f

Lemma 증명) 
    "cyclic 하면 back edge가 있다"(대우)로 증명

Theorem 증명)
    u->v인 상황에서 topological sort가 원하는건 u,v순으로 출력되는것. 
    DFS 수행 시 항상 v.f < u.f

1이 맞다면 2 되는 것 증명)
    u -> v 인 상황에서, v를 만났을 떄,
    backedge가 없다 = gray일 수 없다
    따라서 white이거나 black
    black이면 이미 finish time 찍힌거니 참
    white인 경우도 마찬가지

=> DFS 이용해 topological sort 하는것이 옳다

📌 왜 topological sort가 되는지 직관적인 이유

1. in-degree가 0인 것을 좌측에 위치시킨다.
2. out-degree가 0인 것을 우측에 위치시킨다.
3. 그래프 G에대해 DFS를 실행 후 finish time의 오름차순으로 우측부터 위치시킨다 = finish time 빠른게 맨 마지막

출처 : 2023-2 ITE2039 수업