What is Image Filtering?

Image filtering:
local image data로부터 새로운 값을 얻어내는 function.
굉장히 많은 방법이 있지만 심플한 것 배울것

Linear Image Filtering

non linear 한 것도 많지만 이번 수업에선 단순한 linear 한것 볼것임

weighted sum 하는 것을 통해(가중 합) 값을 하나 얻을 수 있음. (convolution) → 단순한 연산

image filtering 으로 할 수 있는 것들:

  • enhance image
    • 노이즈 제거, smooth, increase contrast, sharp하게, …
  • Extract information from images
    • Texture, edges, distinctive points, etc.
  • Detect patterns
    • Template matching

(심플 리니어 필터로도 많은 것을 할 수 있음)

Point Spread Function (PSF)

: A linear function for the image filtering

(‘point spread’ function)

psf라는건 심플한 리니어 필터인데,

psf를 위해서는 커널 필요하고, 커널 모양에 따라 값이 변함.

4

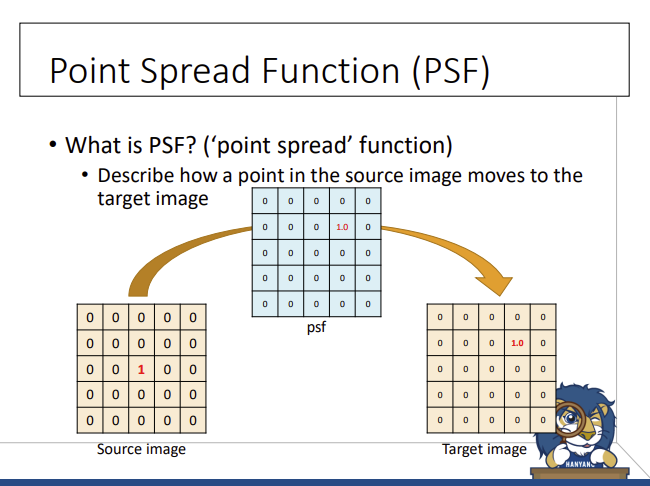
중앙 파란색 → 필터(= 커널)

추가 질문)
Q. PSF의 연산

A. 가중 합과 다른 것임!!

source image에서 값이 있는 부분에만 필터 값 적용함.

이미지에서 값이 어떤 것이 되었던 간에 유무만 판단하여 적용.

그리고 소스 이미지에서 값이 있는 픽셀의 개수만큼 타겟 이미지의 갯수가 생성이 되고, 이들의 합이 output이 된다.

Formulation

그리고 이 메카니즘을 수학적으로 표현하면,
(수학적 definition)
-> G = H * F

5

수학적 정의만 봐서는 결과 어떻게 나올 지 모름

6

[psf wiki]

주어진 커널 모양으로 이미지가 퍼저나감. 그래서 이름이 ‘포인트 스프레드 커널’

Convolution

7

실제로 두번째 줄 적용하면 컨볼루션 결과 얻을 수 있음

하지만 다른 방법으로,
H라는 이미지와 F라는 필터 있을 때
필터 뒤집고, cross correlation 구하면 컨볼루션의 결과 얻을 수 있음

Cross-correlation

8

Measure of similarity of two inputs(signals)

element wise로 곱한다.

(연산 속도는 더 빠르지만 convolution이 직관적으로 필터 적용이 이해가 됨.)

Convolution vs. Correlation

9

Convolution:
점이 어떻게 퍼저나가는지에 대해

Correlation:
두개의 데이터가 얼마나 비슷한지 측정하는

하지만 좌우 상하 뒤집은 커널 적용하면 컨볼루션과 같은 결과

Q. 결국 컨볼루션은 cross correlation을 필터 뒤집어서 하는 것..?

A. 식은 다른데 결과론적으로 봤을 때 cross correlation의 필터 뒤집어서 적용하면 컨볼루션의 결과가 된다.

Q. cross-correlation 연산이 왜 convolution보다 효율적인가?
(가운데 한 값을 구하기 위해 convolution을 사용하면 두번 연산 후 더해야하는데
cross correlation 적용 시 뒤집어서 한번만 하면 되기 때문에 연산 간단하다?무슨 뜻?)

A.
convolution은 한 픽셀의 값을 결정 할 때 주변 픽셀들이 영향을 줌. 한 픽셀을 봐도 마찬가지. 필터가 겹치는 경우 그 픽셀에 대해 영향을 줌.

하지만 cross correlation의 경우 같은 연산인데 output기준으로 생각.

필터 상하 좌우 뒤집어서 연산을 하면 output특정 픽셀에 대한 결과를 convolution한 번 한것과 같은 연산 노력이 들어감.

결국 하나의 픽셀에 대해 연산 결과를 원할때에는 convolution은 주변 모든 픽셀에 대해 연산을 필요로 하지만 cross correlation의 경우 연산이 훨씬 간단함.

Denoising

:노이즈 제거하는 것

여러 프레임 캡쳐 후 노이즈 제거하는방법 어려움(여러 프레임 평균)

따라서 싱글 이미지로 해결하는 방법 찾고자 함.(한 이미지의 주변 픽셀 평균)

평균내서 노이즈 제거 가능한데,
이를 convolution으로도 연산할 수 있음

  • 더 큰 필터 사용 시
    • 노이즈는 줄어들지만 blurry해짐
  • 박스 필터값의 합이 1인 이유
    • 합이 1이 넘으면 전체 밝기가 밝아지고, 1보다 작으면 갈수록 어두워짐
    • 합이 1이되면 전체 밝기 유지됨

10

More convolution examples

  • 엣지 찾기
    • 1,-1인 horizontal gradient 필터 적용 시
      인접한 두 픽셀의 밝기 차이 표현됨.
    • -I(x,y)+I(x+1,y)
    • -I(x,y)+I(x,y+1)

  • Sharpening 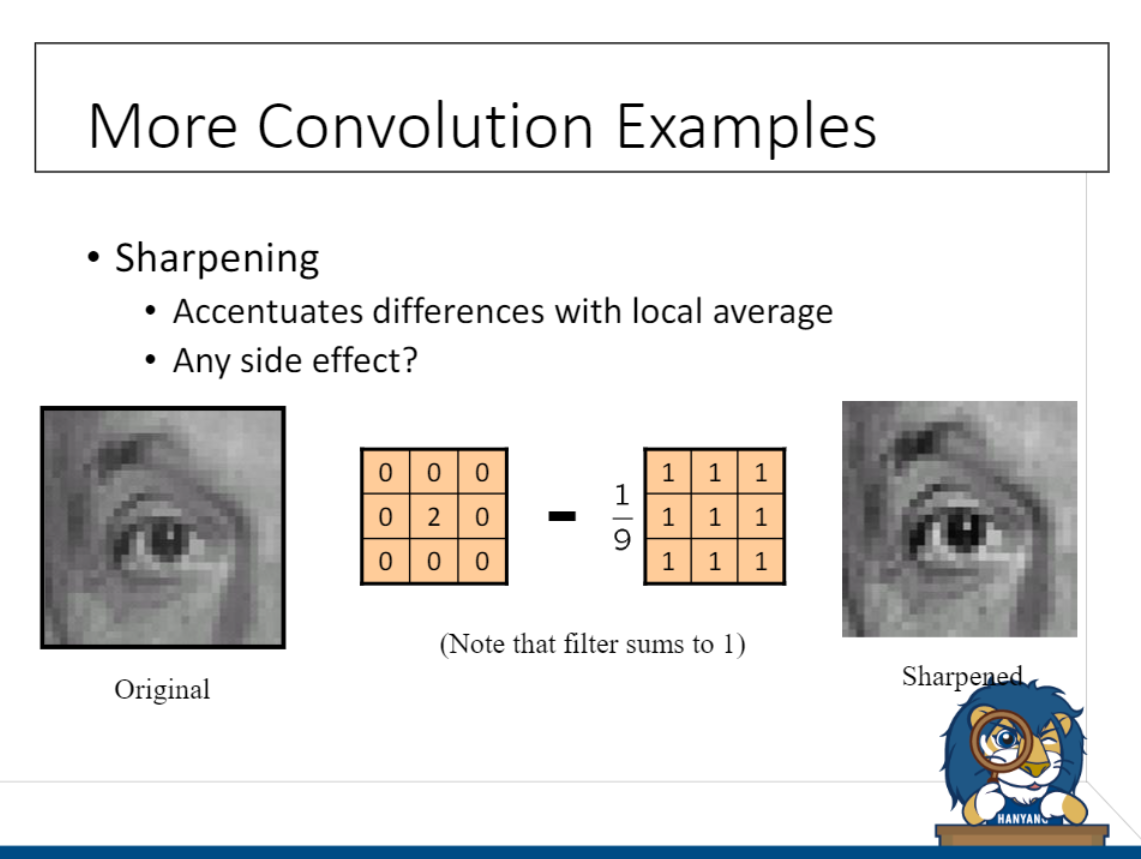11 2배로 밝기 키우고, 그 버전에서 블러링 버전을 뺀것.

  • Properties 12

컨볼루션은 linear 연산이라고 이야기 했었음.

컨볼루션이 그냥 opertion이 아니라 결합법칙, 분배법칙등이 모두 적용되는 유용한 연산.

Practical Matters: Padding

가장 바깥쪽 픽셀은 컨볼루션 연산 불가.

컨볼루션 계속 진행 시 이미지 계속 작아지는 문제 발생할 수 있음

따라서 패딩을 붙여줌.

다양한 방법 있는데 보통 0을 주변에 붙이는걸 많이 씀

13

Q. 그래서 왜 convolution??

기존 logistic regression에서
$x’ = W^Tx + b$ ->linear transformation
$x’’ = \sigma(x’)$
에서, $W^Tx$ 이 부분을 w*x로 바꿔서 생각

[출처1]ITE4053 수업