목차

  • illuminasion != brightness
  • 무엇이 pixel의 brightness 결정하는지
    • $L, \rho, V$
  • 사람 눈에 들어오는 빛인 illuminancy에 영향을 미치는 것들
    • $I(\lambda) = \rho(\lambda) L(\lambda)$
  • brightness / contrast
    • Weber’s Law
  • Photosensitive Cells
  • Brightness Contrast and Constancy
    • brightness contrast
    • brightness constancy
  • cones
    • 어떻게 rgb 값으로 계산되는지
    • $\alpha_{i}(C) = \int_{\lambda_{min}}^{\lambda_{max}} S_{i}(\lambda)C(\lambda) d\lambda,$ $i = 1,2,3$
    • 계산 간단하게 하기위한 방법
  • RGB, CMY, HSI
    • Intensity, Saturation, Hue
      • 각각이 무엇이고 작은 값과 큰 값 가지게 되는 경우
  • 카메라가 이미지 받을 때
    • Demosaicing
    • Bayer filter
    • dimension 변환
  • Image Colorization
    • 사용할 수 있는 objective function
      • L2 loss
      • multinomial classification
        • input, output 크기(작동 구조)
  • Inherent Ambiguity
    • Diverse Colorization
    • Language Based Colorization
    • Exemplar Based Colorization

illumination, brightness

1

  • illumination
    실제 픽셀 값(위 이미지의 A와 B 같다고 판단)
  • brightness
    What we feel(위 이미지의 A와 B 다르다고 판단)

$\because$ 사람은 조명과 물체 decompose 하는 능력 있음.

2

Radiometry

(무엇이 pixel의 brightness 결정하는가)

3

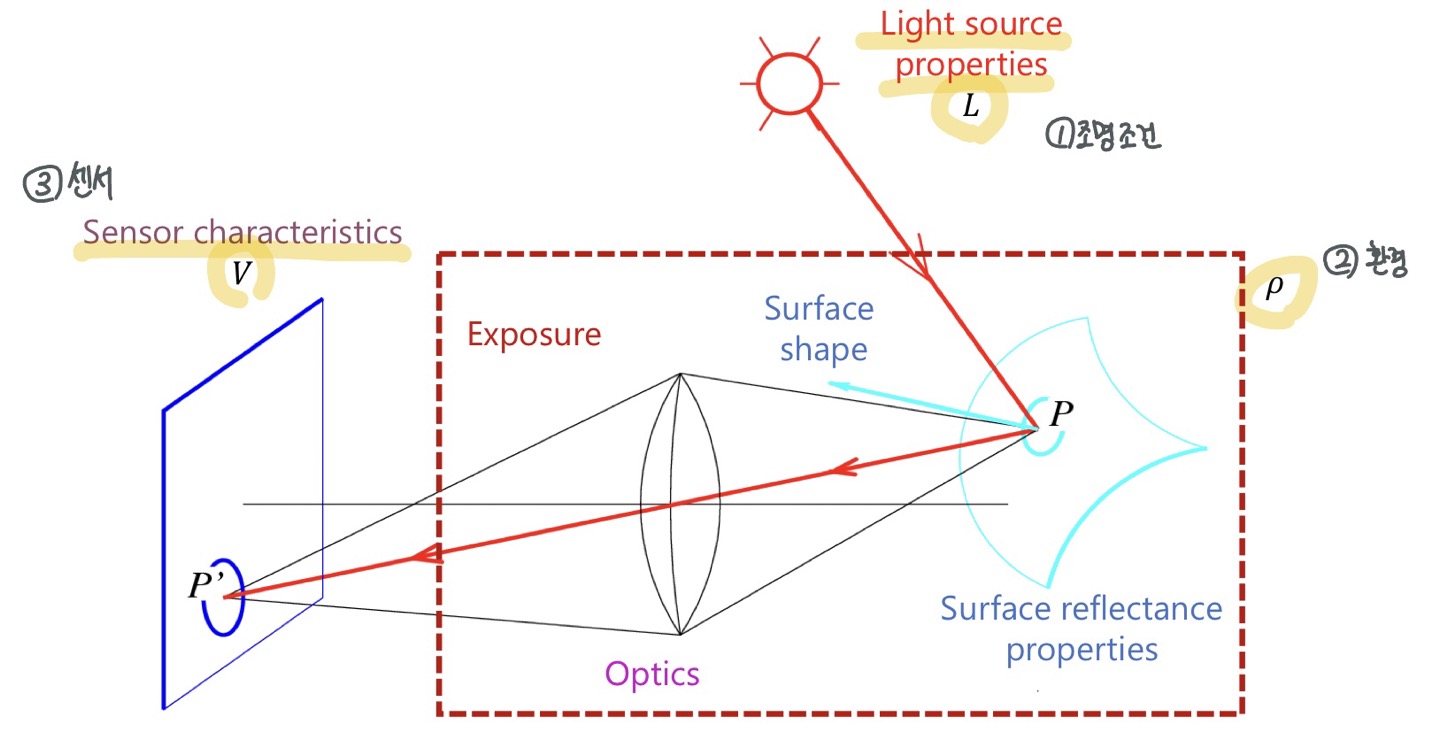
중요 세가지

  1. 조명조건: 색깔 세기 등
  2. 환경적인 요소: 물질의 특성, 보는 각도, 물체와 카메라의 특성들, 카메라 자체의 노출과 관련된 특성 등 -> 이 챕터에서는 하나로 모아 $\rho$ (/rho/) 로 표현
  3. 센서(사람으로 보면 시신경)에 따라 intensity, 색상 등 결정

사람눈에 들어오는 illuminance $ I $

물체로부터 받은 light(Illuminance): \(I(\lambda) = \rho(\lambda) L(\lambda)\)

L(λ):

  • 표면의 입사된 빛의 양
  • Incident energy distribution

ρ(λ): Reflectance(albedo)

  • 표면에서 반사되는 입사광의 비율.
  • 물체의 반사율, 투과율

4

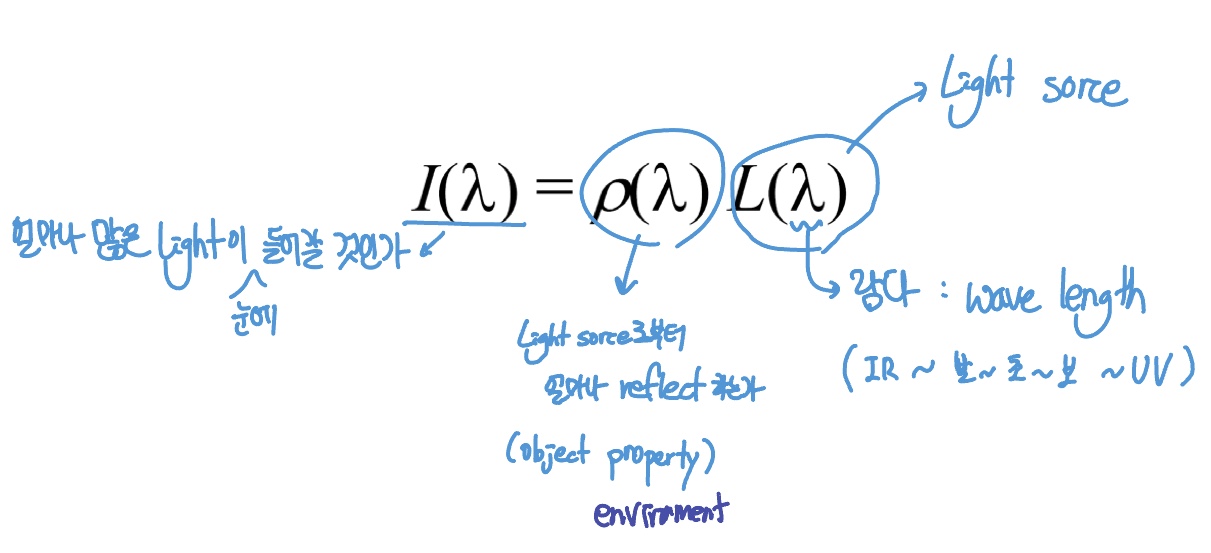
visual system이 light source로부터 받는 에너지 Luminance(or Intensity)

⭐
$ f(x,y) = \int_{0}^{\infin}I(x,y,\lambda)V(\lambda)d\lambda $

이때 $I(\lambda) = \rho(\lambda) L(\lambda)$

실제 pixel value인 f(x,y)를 구하는 것.
Illuminance $I$와 얼마나 민감한지 나타내는 $V$ 곱해서 integrity

빛의 세기와 센서 값이 정해져 있으면 luminance 구할 수 있다(?)

$I$: Light distribution received from an object
$V$: Luminosity function (Relative luminous efficiency function of the visual system)

Photosensitive Cells

망막 retina에 있는 두 photosensitive cells
-> rods and cons 이 두가지가 빛을 인지하는 세포.

  • Rods(간상체) -> Intensity
  • Cones(추상체) -> Color

5

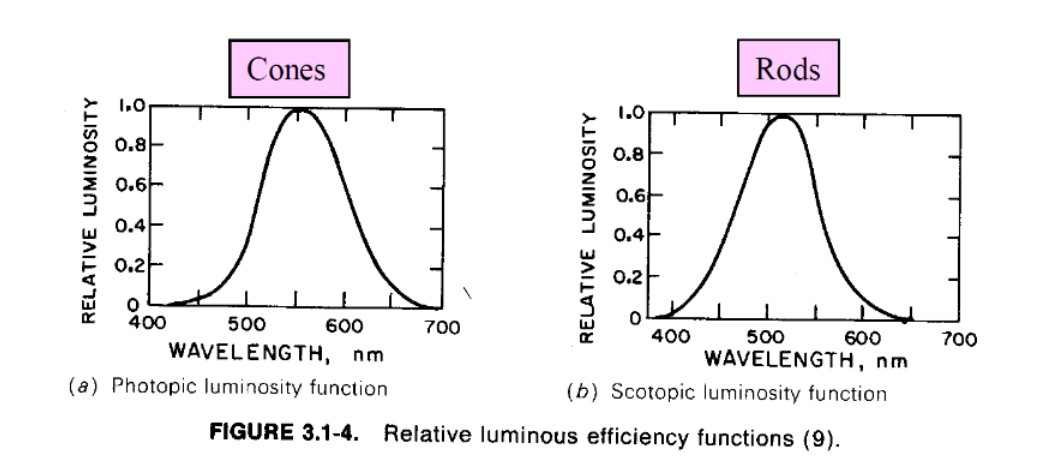
두 세포가 다른 sensitivity, range 가짐

Brightness Contrast and Constancy

: (사람은 luminance로부터 brightness 정하는 한 단계가 더있다.) brightness는 빛 하나만 보는 것이 아닌 주변 surrounding을 같이 본다.

brightness contrast

: 같은데 다르게 보는 상황

ex) 사람은 실제 조명이 무엇인지를 예측하는 부분이 있기 때문에,
주변이 어두우면 어두운데서 찍었다고 생각해서 물체가 실제보다 어둡게 나왔다고 processing.
반대로 전체적인 밝기가 bright-> 밝은데서 찍었다 -> 실제 object는 더 어둡겠구나 라고 process.

brightness constancy

: 다른데 같게 보는 상황

ex) 검은색과 흰색이라도 어두운곳에서 찍은 검은 물체, 밝은곳에서 찍은 흰색 물체가 있을 때 픽셀값은 다르지만, 실제 오브젝트 색이 뭔지 생각을 하는 보정을 거치면서 둘 같아보이는 경우.

Brightness / Contrast

Brightness

: 우리가 실제 감지하는 것
(주변 luminance에 따른 감지한 luminance)

Contrast

Weber’s Law: 실제로 빛의 세기에 차이가 느껴지는 정도는 현재의 세기에 정비례한다.

현재 밝기가 충분히 밝은 경우 여기서부터 차이가 느껴지려면 이것보다더 많은 차이가 있어야 차이가 지각된다.

6 7

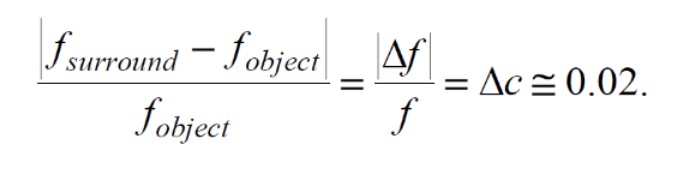
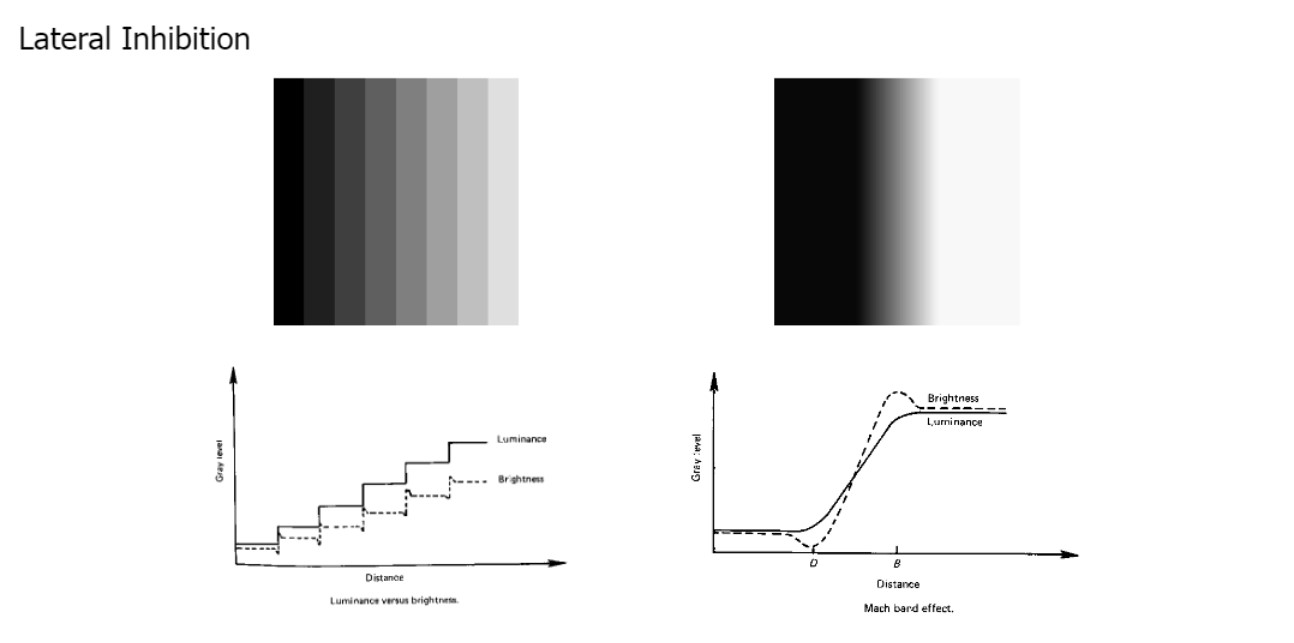
따라서 실제 픽셀의 밝기(그래프의 실선)와 우리가 느끼는 밝기(그래프의 점선)에 차이가 발생한다.

Visible light
Color

3 Types of Cones

8

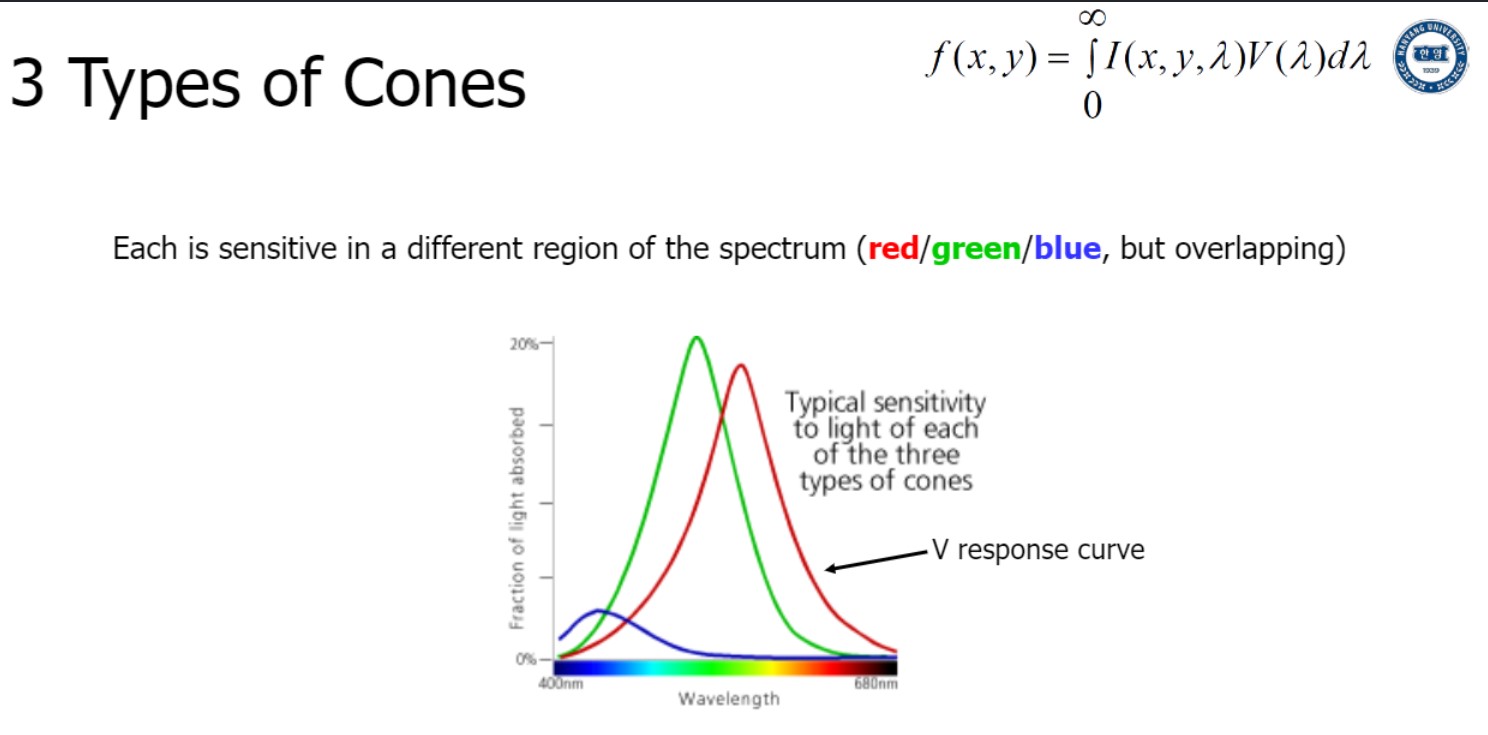
빛을 인지하는 세포 중 색상을 인지하는 세포인 Cones에 세 종류 있다. 각각 Red, Green, Blue 인지.

이 셋은 different cones with different sensitivity.

9

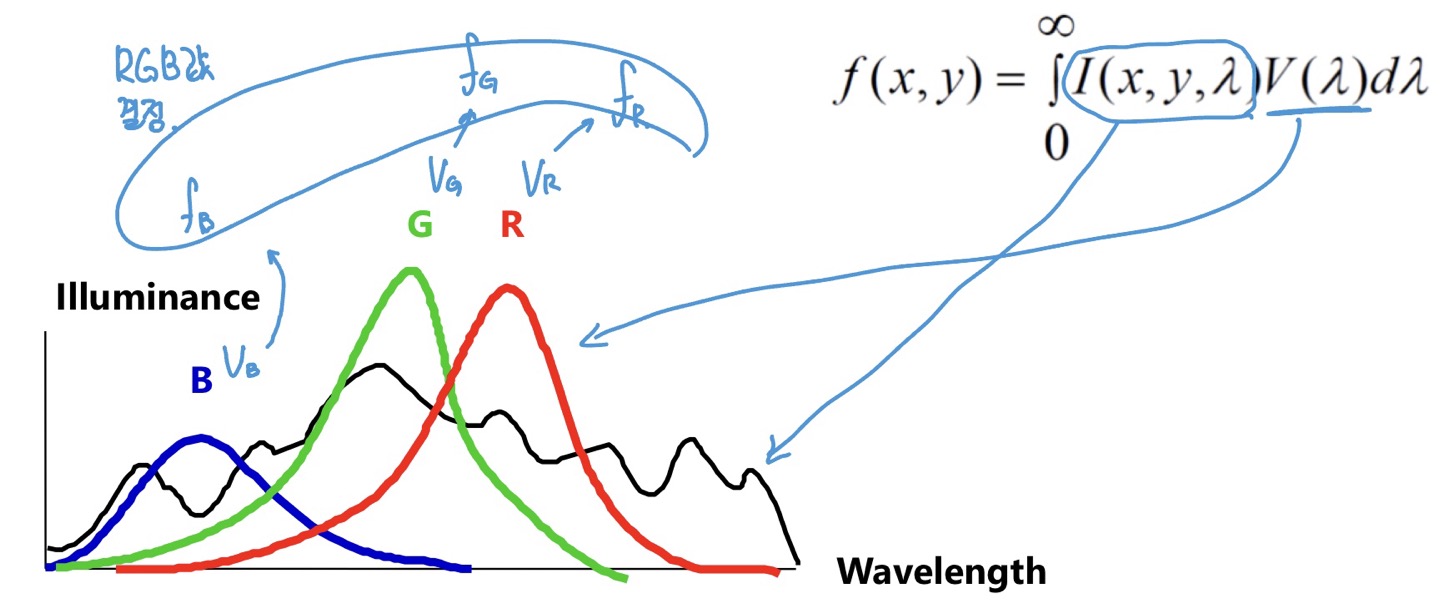
우 상단의 수식에서 $V(\lambda)$ (= 얼마나 민감한지)가 그래프의 각 cone에 해당.

사람눈에 RGB센서가 있어 우리가 색 표현 하는데에도 RGB 표현법을 사용한다.
(3개의 cone이 있는 human visual system과 유사하게)

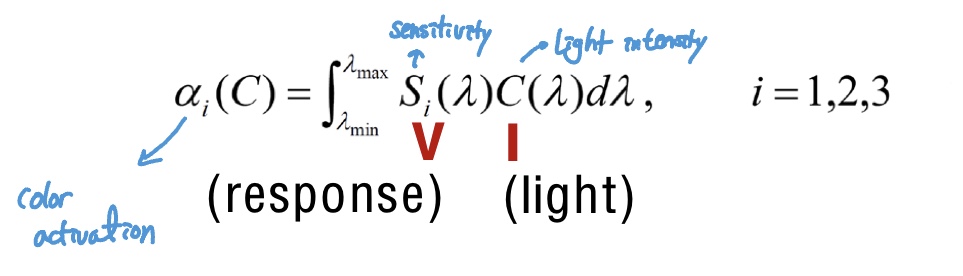10 (i-th cone response)

notation V -> S, I -> C로 변경

R값 구하기 위해서 $\int_{\lambda_{min}}^{\lambda_{max}} V_{R}I d\lambda$
G값 구하기 위해서 $\int_{\lambda_{min}}^{\lambda_{max}} V_{G}I d\lambda$
B값 구하기 위해서 $\int_{\lambda_{min}}^{\lambda_{max}} V_{B}I d\lambda$

Q. 하지만 매번 $S_{i}$(response) 알아야하나? (integration 복잡)
A. NO! 매번 적분하는 것이 아닌 수식 단순화 하는 법 있음

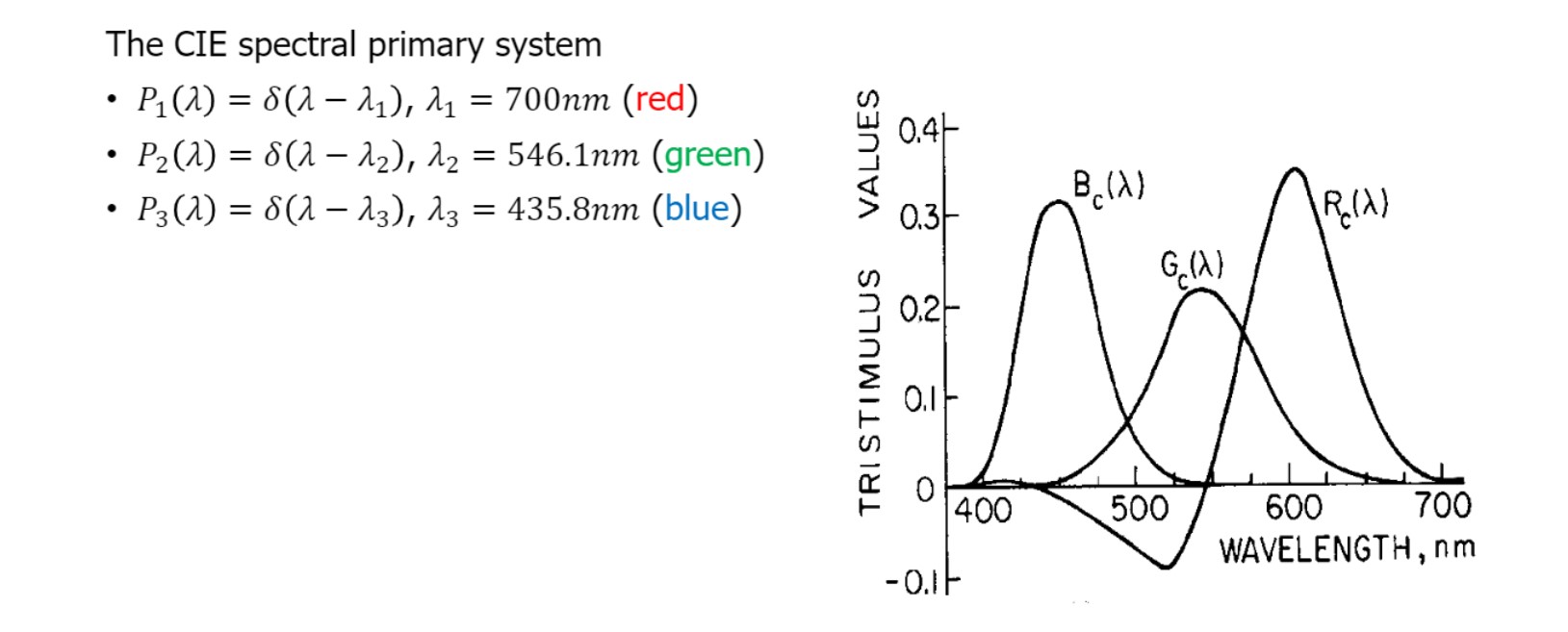
Color matching ⭐⭐

11

** 디렉델타함수도 찾아보기

12

수식 부분,,

  • Grassman’s law에 의하여,
    3개의 primary light source를 섞으면 어떤 색이던 만들 수 있다.

  • Luminanceof a color mixture == sum of the luminance of its components

13

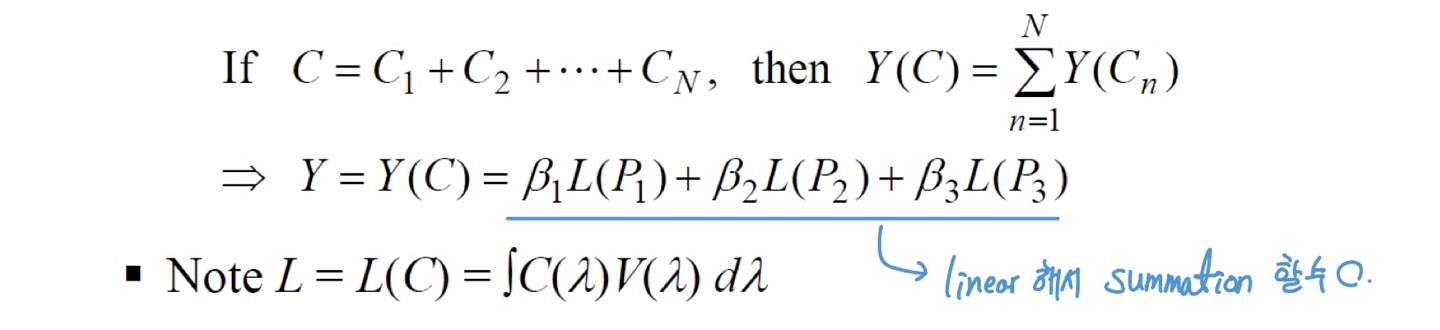
RGB - CMY

14

RGB 뿐만 아니라 CMY로도 표현 가능
$ \because$ linearly independent

Intensity, Saturation, Hue

  • linear 하지 않더라도, 어떤 색이던 3개의 다른 variable로 표현 가능

15

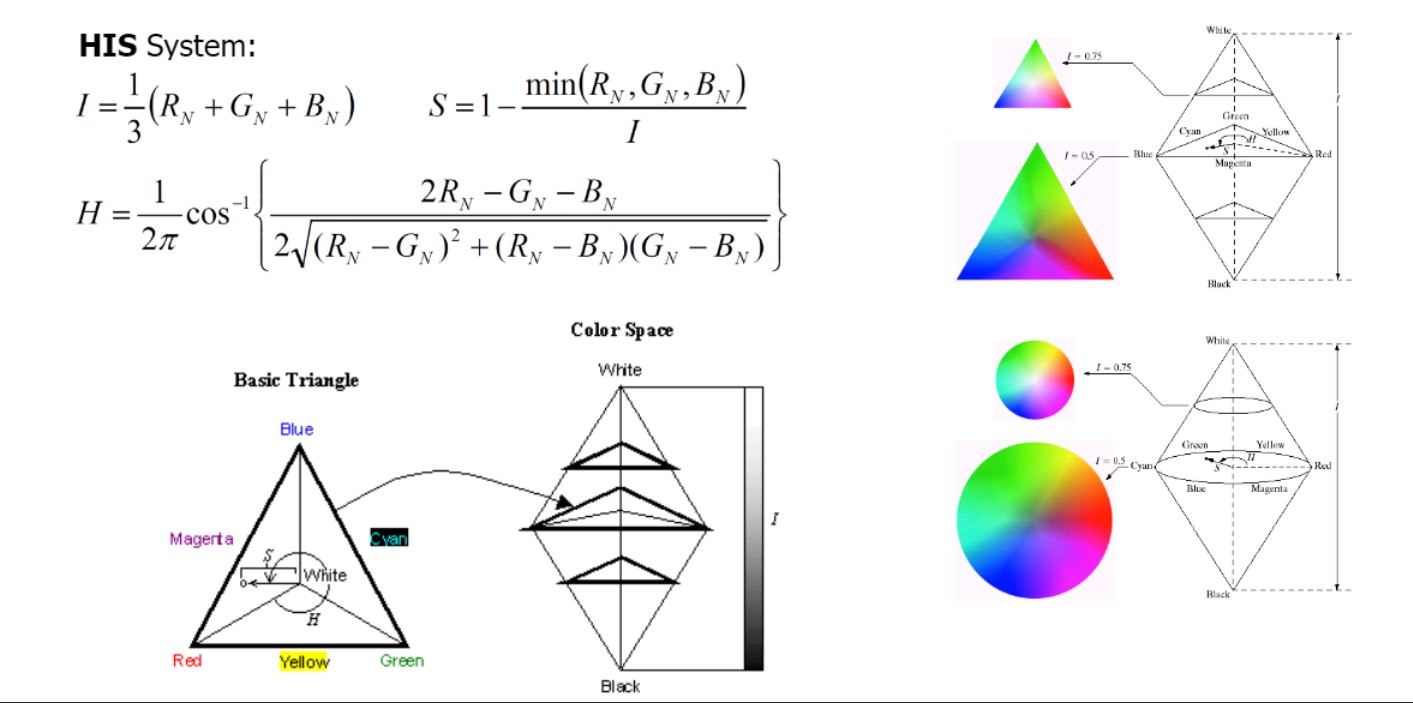
  • I: Intensity
  • S: Saturation (Magnitude. How strong is the color is)
  • H: Hue (What is the color)

S가 최소값을 가지려면, 3개의 color가 uniformly distributed인 경우.
$S = 1-$ ${min(1/3,1/3,1/3)}\over{1/3}$ 이 경우 S = 0

$S = 1-$ ${min(1,0,0)}\over{1/3}$ 이 경우 S = 1

polar coordinate으로 색 표현하고 싶을 때, HIS가 답이 될 수 있음.

RBG space와 linearly transform 하지 않더라도 3개의 variable이 있다면 색을 unique하게 결정할 수 있음

16

예시를 보면,
Intensity = 세 color의 평균 Saturation = 색이 얼마나 strong한지.
Hue = 무슨색

왜 HSI 쓰는지
RGB 표현으로는 단순히 hue 조절을 하기가 힘들다.
하지만 hsi에서는 angle 바꾸면 된다.
마찬가지로 saturation도 RGB에서는 복잡한 연산 해야함.

정말 다양한 color coordinate system있음 대부분의 color system은 linear transform을 통해 연산할 수 있음
(하단 연산처럼)

17

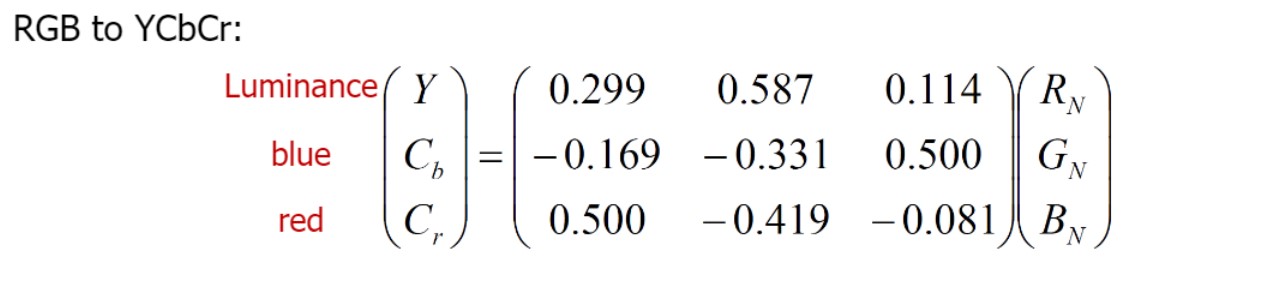
단순히 matrix multiplication으로 변환 가능

Color in cameras

  • Demosaicing: 카메라가 받은 각 화소별 값을 이미지로 변환하는 것

  • Bayer filter로 받은 픽셀은
    G R
    B G
    이런 형태.

  • 2W x 2H -> W x H x 3 형태 변환.

Demosaicing 전후 프로세스 추가 설명 참고 링크

Image Colorization

: 흑백 이미지에서 어떻게 컬러 이미지 얻는지에 대해 배움

기본적으로 딥러닝으로 예측한 것.

<FCCB 2016> - 딥러닝 based colorization의 첫번째 버전 18

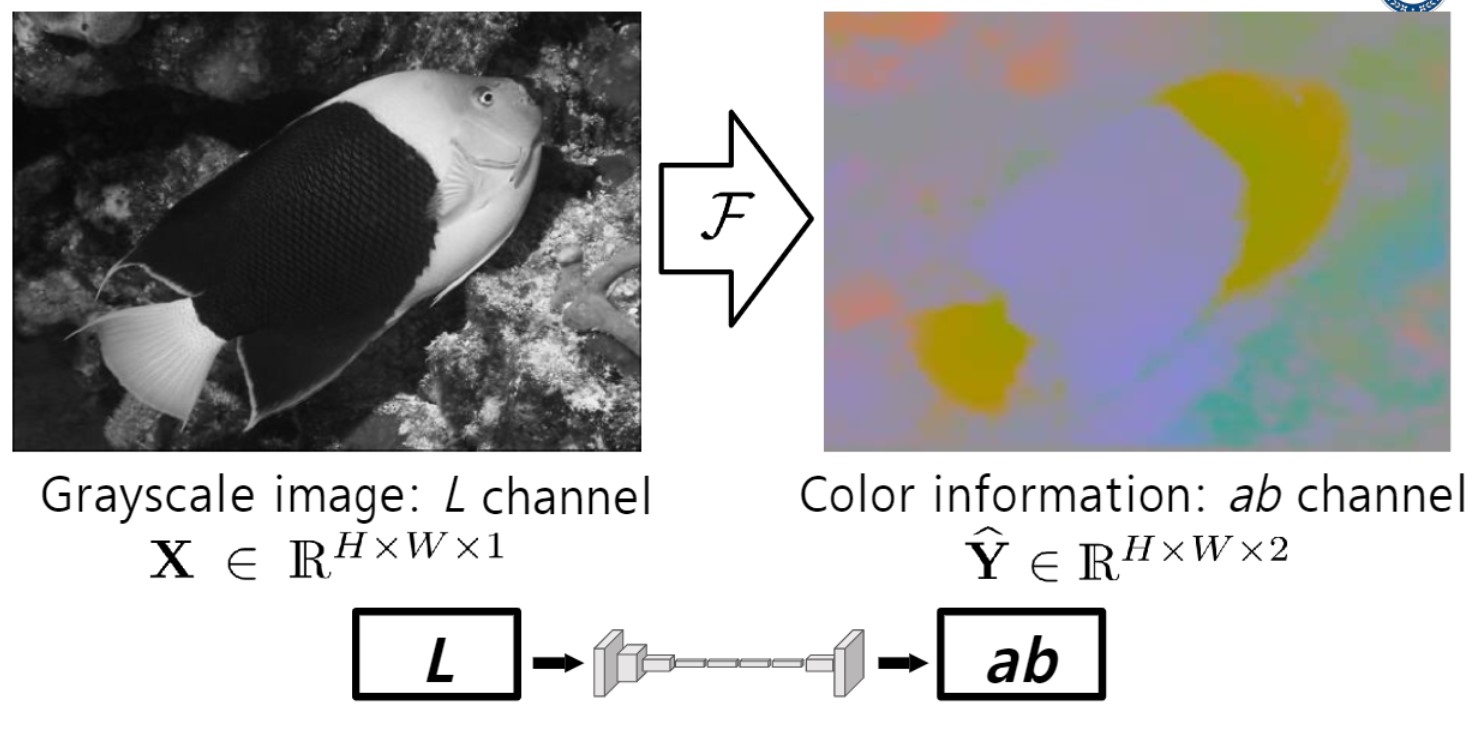
Single channel을 딥러닝 모델로 넘기면(input. 세 채널 있어야 하는데 현재 두 채널 부족한 상태.),
(a, b)두 채널을 리턴 함. (참고로 LAB 컬러 표현법)

19 이후 리턴 받은 (ab)와 L 합치면(Concatenate) 최종 결과.

LAB 색 표현법
a는 초록에서 빨강 축, b는 파랑에서 노랑 축,
l은 밝기

이러한 딥러닝 모델을 train 하기 위해서 어떤 objective function($\supset$ 손실함수) 쓸 수 있는지

20

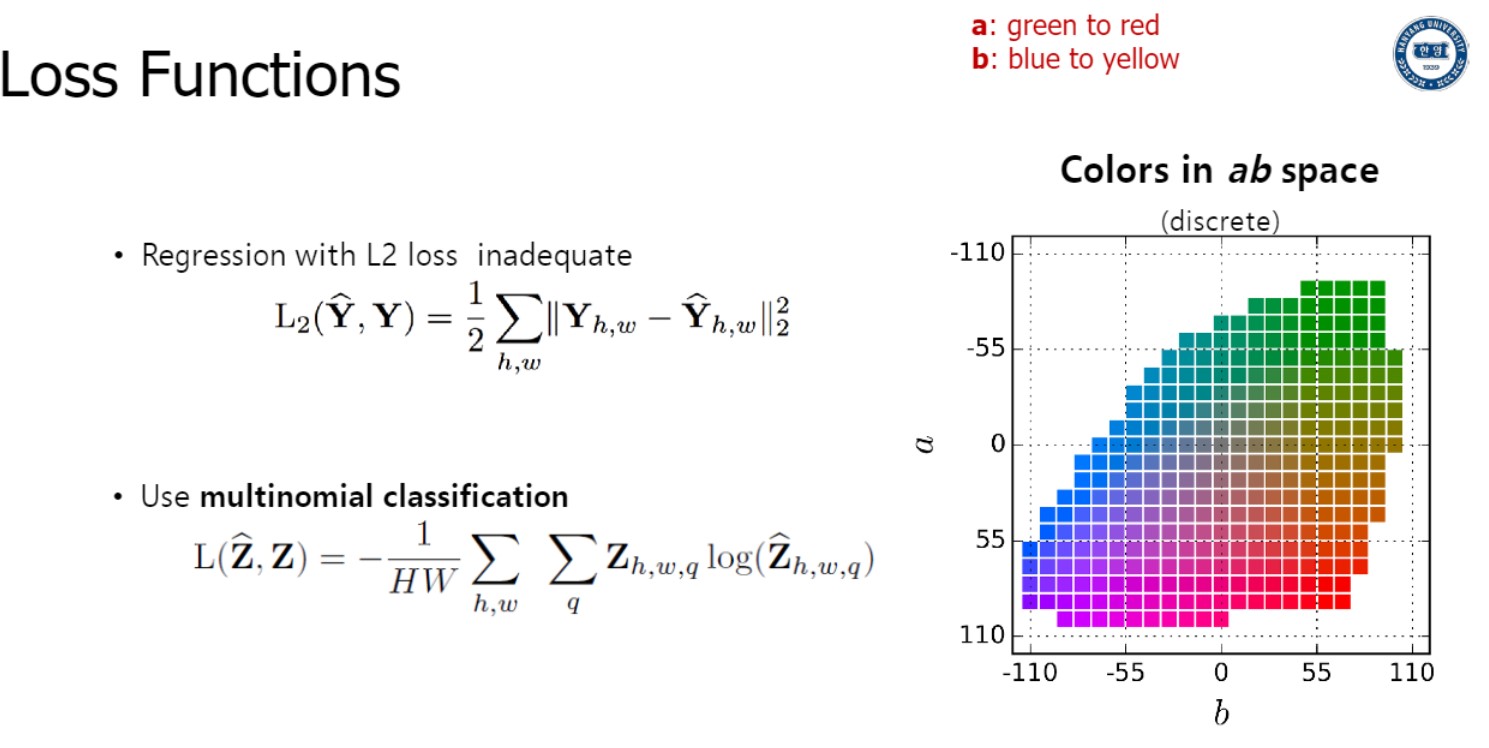
  1. 가장 단순한 방법은 regression loss 사용하는 것

Ground truth인 $Y_{h,w}$와 예측한 값인 $\hat{Y}{h,w}$의 L2 distance 구해서
모든 픽셀에 대해 비교하여 평균을 내면,
loss function인 $L{2}(\hat{Y}, Y)$ 구할 수 있다.

  1. classification방식으로 train

(위에서 본 FCCB 2016 모델이 작동하는 방식)

LAB color space는 위 이미지의 우측에있는 것과 같이 a 값과 b 값에 대한 rgb값이 lookup table로 있음. 각 값을 quantize하여 313개의 color 값을 얻을 수 있다.
결국, (이미지 classification하는것과 같이) “cross entropy loss function for pixel level classification over 313 color”

이미 ground truth가 있음(rgb값)
각 픽셀에 대해 얼마나 잘 예측했는지,
그리고 regression보다 classification이 ML 더 잘 훈련해서 색 예측 문제를 classification으로 풀었음.

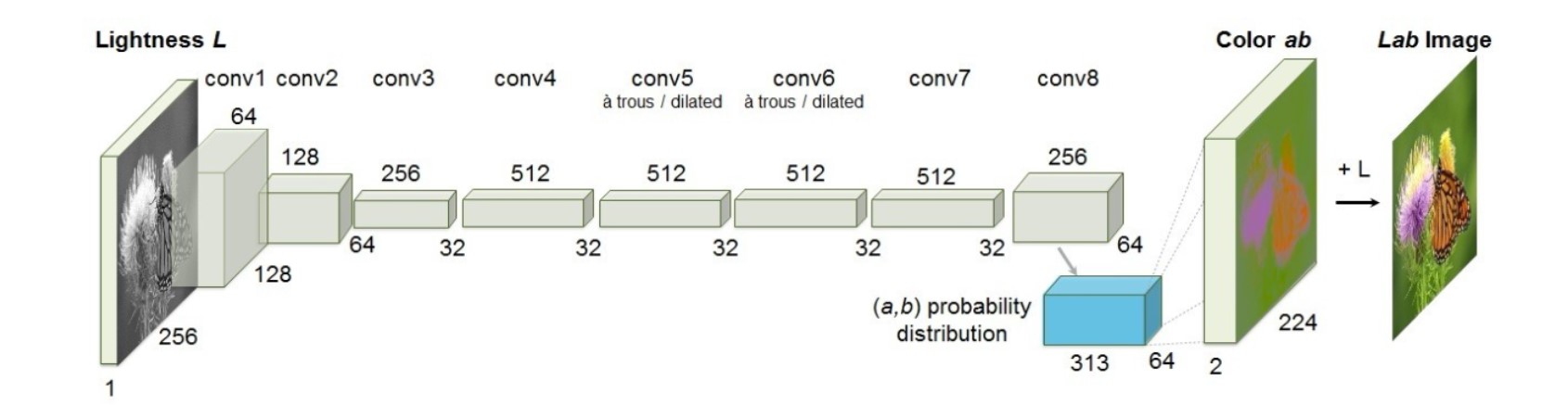21 input, output 보기

input
= 256(dim) x 1(single channel)의 luminance value

output
(파란색 직육면체 부분)
= 64 x 64 x 313(class prediction for every pixel)

(다음 단계)
각 픽셀에 대해 class prediction 한 값을 위에서 말한 lookup table에 기반해서 rgb 색상으로 나타낼 수 있음

(최종 단계)
이후 L 값과 concatinate하여 최종 결과 얻는다

Colorization model이 결국 prior knowledge를 learning 하는 것.
예를 들어 나무는 초록, 하늘은 파랑 등등

Inherent Ambiguity

하지만 Inherent Ambiguity문제 존재.
(prior knowledge에서 넥타이는 파랑일수도 있고 빨강일수도 있음) 더 많은 정보를 주어야 함.

Ambiguity 해결법 3가지 ⭐

1. Diverse Colorization

(VAE와 GAN 등) generative model에 기반한 것

22

핵심은 noise input으로부터 probability 학습한다는 것.
(deterministic(결정론적)하게 예측 결과를 주는 것이 아니라)

확률분포를 학습할 수 있음

다시말해서 가우시안으로 분포 예측하고 sampling (추후에 배움)

23

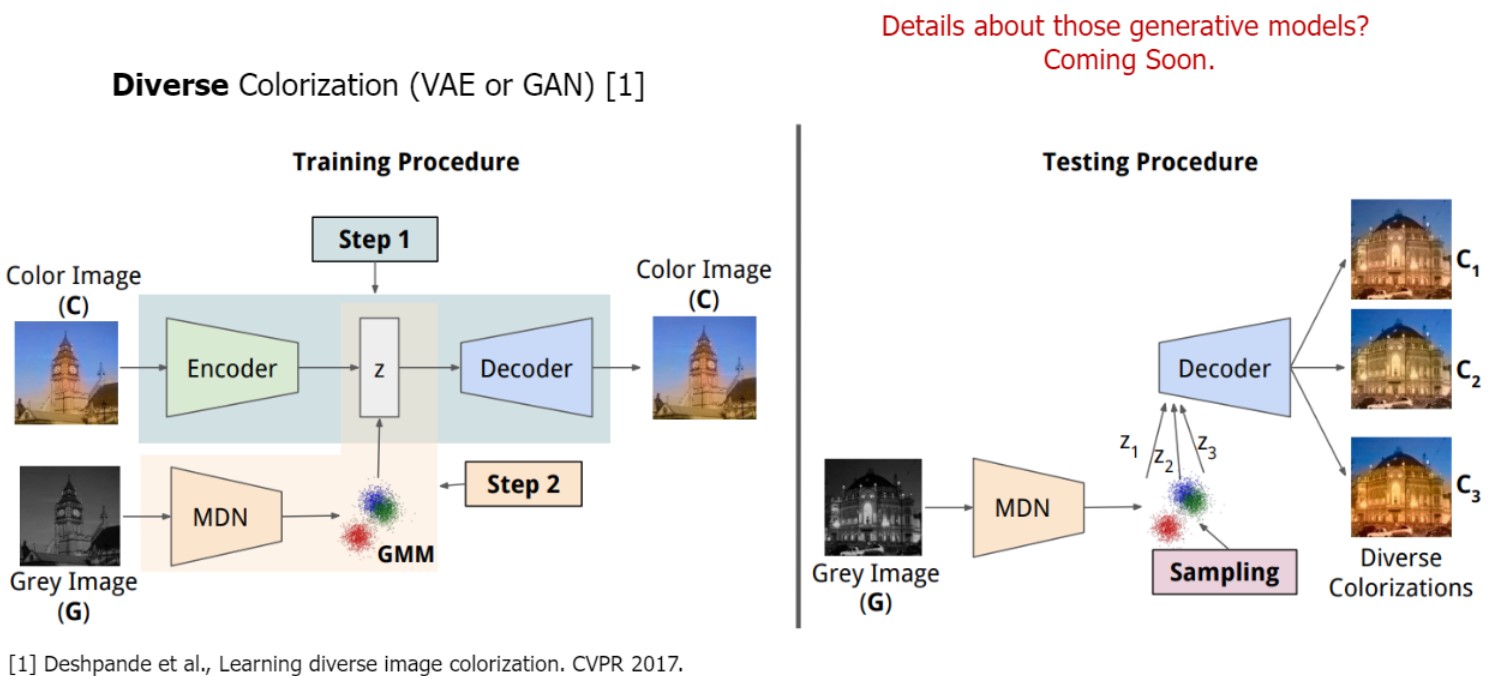
(디테일은 우선 생략)

z값을 determinent 하게 계산 하는 것이 아닌
확률분포(probability distribution)를 predict 한다는 것이 point
(mean, variance 값인)

이 말은 inference stage에서 예측된 distribution을 가지고 sampling 진행.
따라서 같은 이미지를 가지고 다른 z값(이미지)을 얻을 수 있음

왜냐하면 확률분포에서 sampling을 하는것이기 때문

2. Language Based Colorization

“white ship” 등 언어로 추가정보

2425

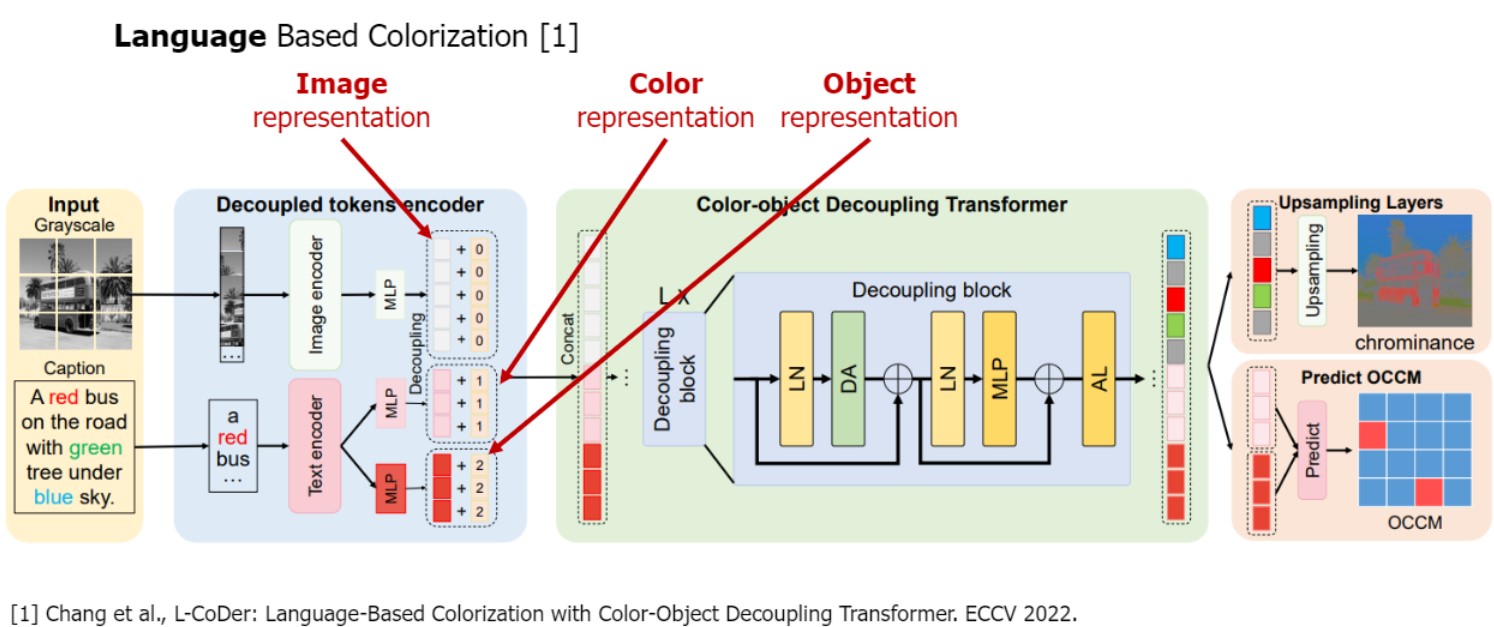
이 task를 해결하기 위한 key issue는
적절하게 caption을 encode하는 것

즉, 주어진 문장에서 color representation 정보를 추출. (예를 들어 버스 -> red, 나무 -> green 등)

이후 colorization step에서는 gray scale image인 image representation과 color representation을 combine해서 최종 colorized 이미지 얻을 수 있다.

3. Exemplar Based Colorization

같은 colorize 할 이미지를 주었더라도
레퍼런스로 준 이미지에 따라 다르게 색 칠함.
additional reference가 적절하게 colorize하기 위한 추가적인 정보

레퍼런스를 바탕으로 빨간 옷 입은 예시 주면 결과도 빨간 옷

2627

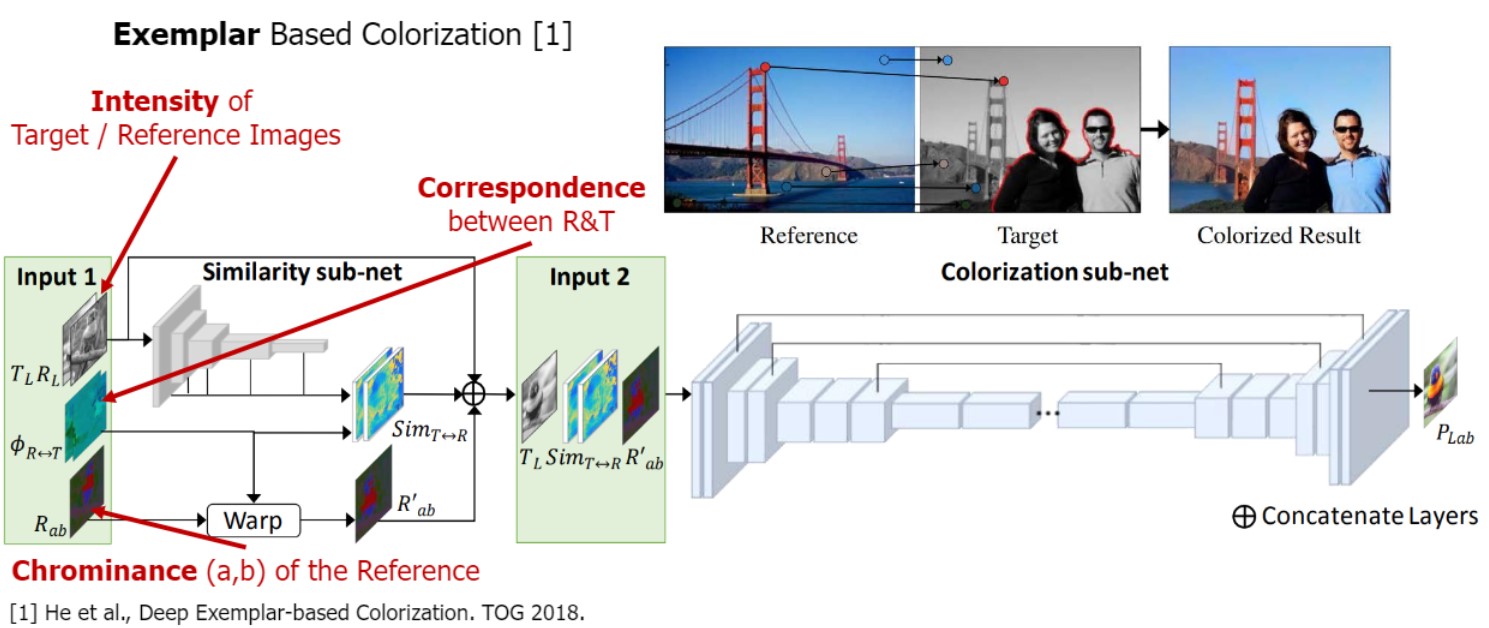
key issue:
레퍼런스 이미지와 타겟 이미지 사이의 correspondence를 적절하게 찾는것

예를 들어, 레퍼런스 이미지의 금문교와 타겟 이미지의 금문교 픽셀의 correspondence를 찾고 color borrow 할 수 있어야 함

출처 : 2023-1 ITE4052 수업