ITE4053_DL> 07-2 Batch Normalization
Batch Normalization
: 굉장히 유명한 approach
data augmentation 누구나 쓰듯 이것도!
- 하이퍼파라미터가 problem search 하는데 훨씬 쉽게함
- Quick & better NN
- hyperparameter에따른 결과 차이 크지 않게 함.
ex) learning rate 0.1이나 0.2나 차이 크면 곤란
but 이것 넣으면 차이 감소
What is batch?
$X = [x^{1} x^{2} x^{3} … x^{m} ]$ size (n,m)
$Y = [y^{1} y^{2} y^{3} … y^{m} ]$ size (1,m)
vectorization은 효과적으로 m개의 train example 계산할 수 있게 함.
하지만 traning very slow.
m개 각각 gradient 구해서 평균값으로 update 하는데, update 한번에 오래걸림.
-> 이 문제 막고자 mini-batch 사용
Batch vs mini-batch
Batch: 한번에 전체 데이터 계산 후 update mini-batch: 1000개씩 5000개의 mini batch $\therefore$ 한 batch(m개중에 1000개) 사용해서 gradient update
hyperparameter 빨리 업데이트할 수 있음
- y(레이블)도 마찬가지로 동일한 크기로 나누는거 잊지말기
표기 알아두기
$x^{(i)}$ : ()소괄호는 training #
$z^{[l]}$ : []대괄호는 layer #
$X^{{t}}, Y^{{t}}$ : {}중괄호는 mini-batch #
One epoch
1000개씩 5000번 진행하는 mini batch가 있을 때
1000개마다 업데이트 하는 것을 5000번 반복하면, train data 전체 한번씩 사용하는 것. => 1 epoch
1epoch = 모든 데이터가 traning에 한번씩 노출되었다.
수업 중 Q.
1000개 data(1 mini batch)써서 업데이트 하면, 다음 batch에 업데이트 된 W, b가 적용?
A. Yes 였던 것 같음
얼마나 오래 학습할 것인가에 대한 것인 epoch도 하이퍼 파라미터
Training with mini-batch gradient descent
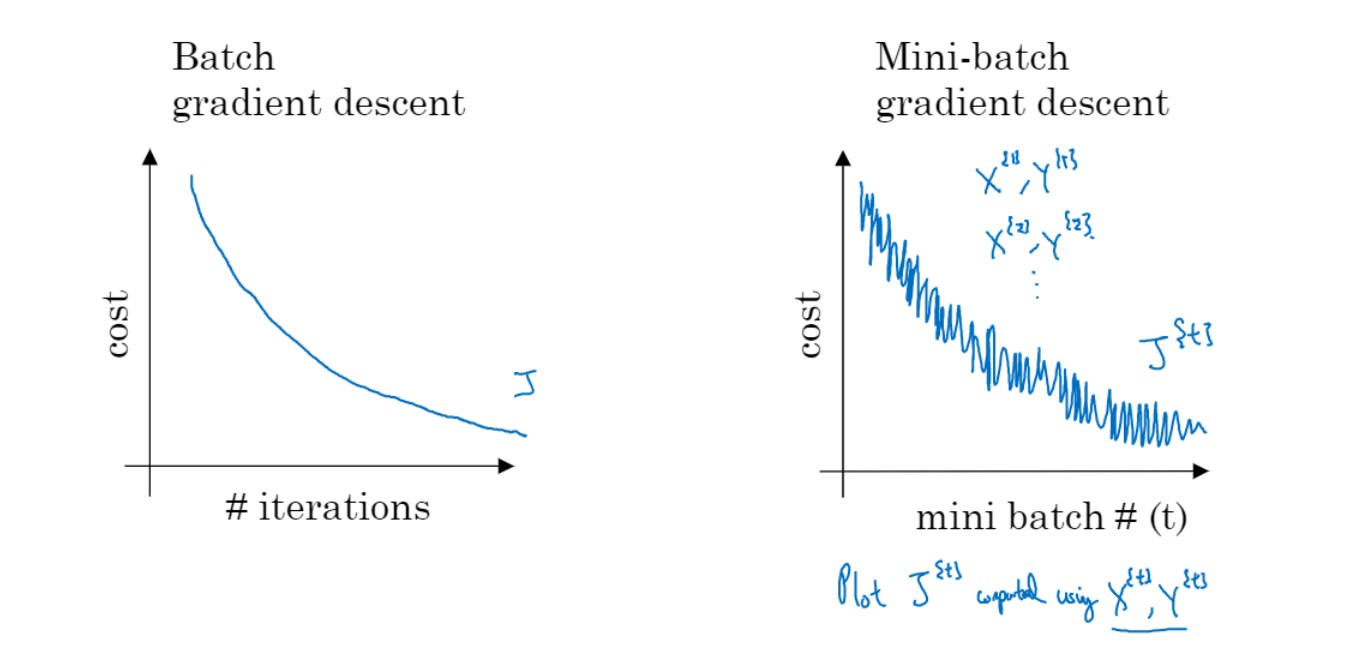
매번 step 마다 mini-batch 단위로 gradient 계산.
이때 noisy 한 이유는,
$\therefore$ 1000개에겐 gradient 감소지만 이후 1000개에겐 증가하는 방향일 수 있음.
noisy 하지만 크게 봤을 땐 감소하는 방향
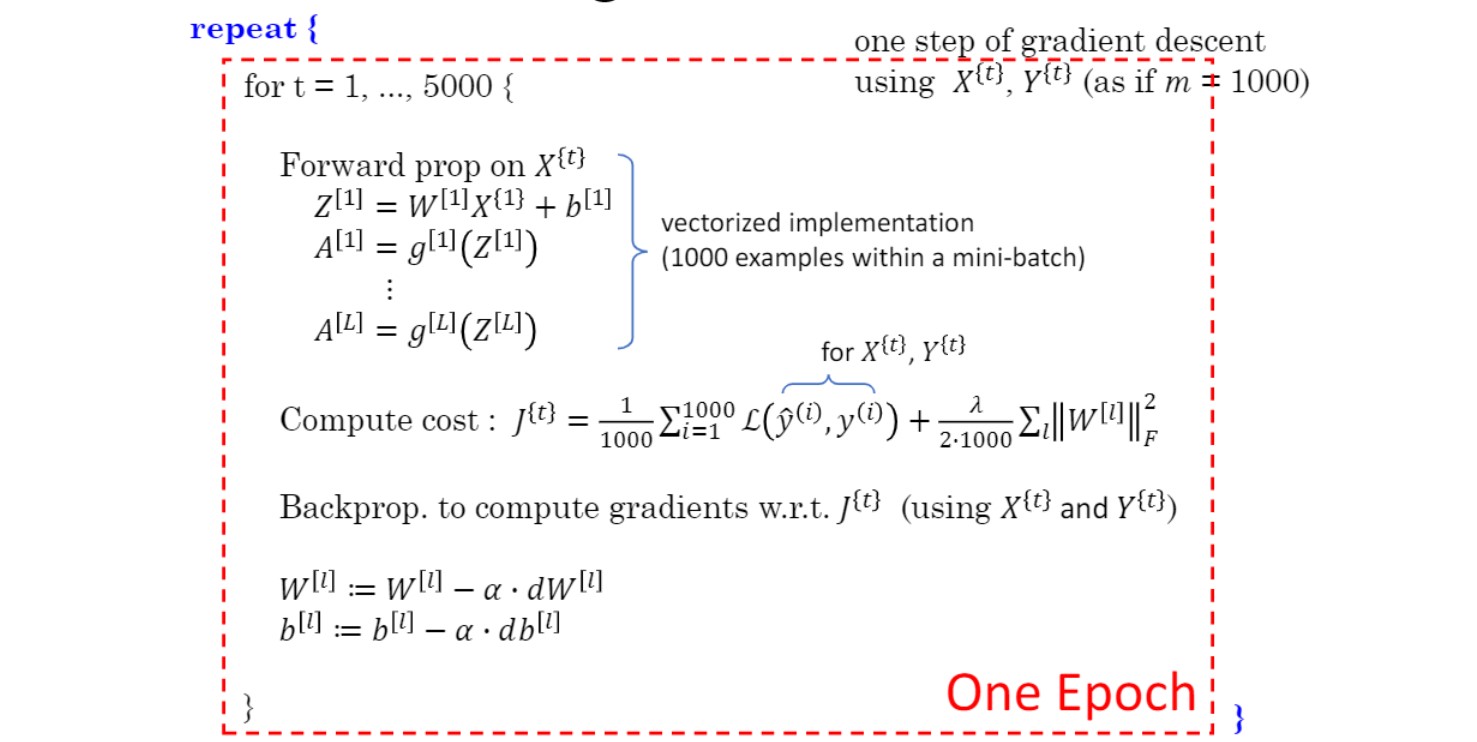
이를 코드로 표현하면 위와 같음.
기존의 하던 순전파, cost 계산, 역전파를 batch 크기의 데이터로 업데이트 후 batch 개수만큼 반복.
Choosing your mini-batch size

mini-batch size가,
너무 작으면 -> 너무 noisy
너무 크면 -> 오래걸림
중간크기가 best

위 이미지에서 x표시 한 곳에서 학습 시작한다면, $M_{L}$ 로 수렴. ( $M_{G}$ 로 와야 하는데)
하지만 Mini-batch 사용한다면, 가끔은 운좋게 Local에서 빠져나와 $M_{G}$ 로 갈수도 O
=> 가끔은 noisy한게 좋을 수도
Training set이 작다면 mini-batch가 아닌 그냥 batch gradient descent를 사용.
mini-batch사이즈는:
-> 64($2^{6}$), 128($2^{7}$), 256($2^{8}$), 512($2^{9}$), 1024($2^{10}$), …
2의 n승 크기로 보통 나눔.
그래야 메모리에 더 잘 fit, (드라마틱 하진 않지만 관례)
수업 중 Q.
mini-batch size라는게 데이터 총 크기? 개수?
A. mini-batch size = number of set.
Implementing Batch Norm
이전에 학습속도 올리고자 input을 normalization했었음.
하지만 $W^{[l+1]}, b^{[l+1]}$ 학습 빠르게 하기 위해
input이 아닌 $a^{[l]}$ normalize할 수 없나?
=> Batch Normalization (input이 아닌 feature map normalize)
이때, feature를 normalize하는데 z, a라는 선택지 2개가 있음.
하지만 경험적으로 Z가 더 나았다.
$\therefore$ 요즘 보통 z normalize
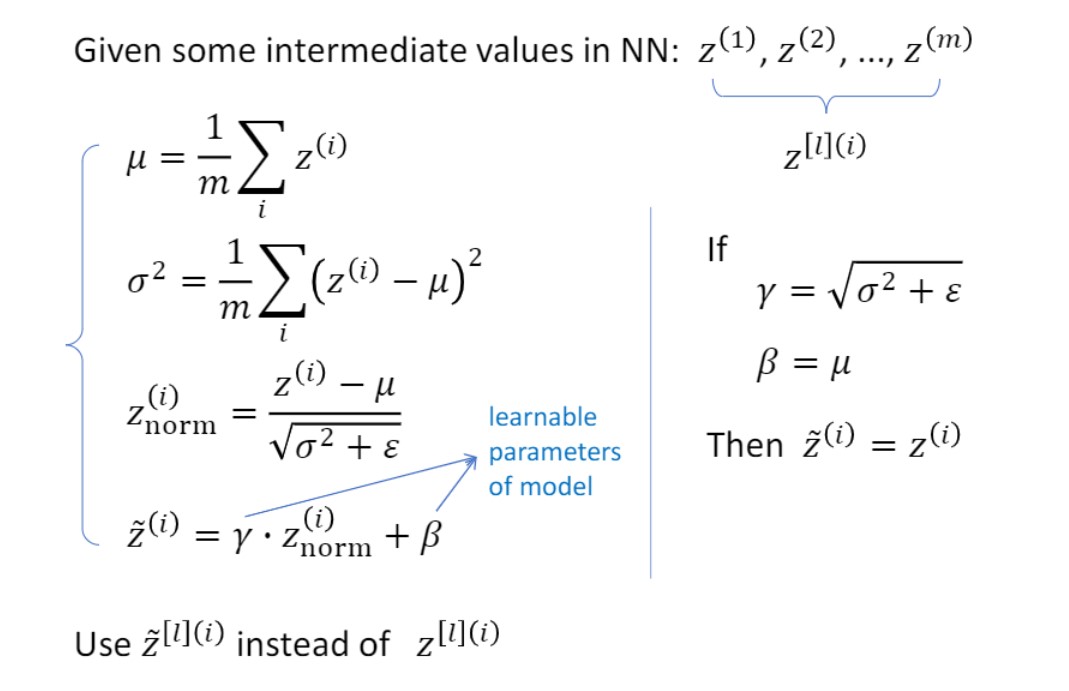
아직 어떤 값으로 정규화를 시켜줄 것인가에 대한 문제가 있음
평균이 0인게 좋을수도 있지만 0.7이 나을수도 있고,,
분산도 2가 좋을수도 있고 1.5가 좋을수도 있고,,
이렇기 때문에 mean과 variance도 trainable한 파라미터로 설정.
$\beta:$ 평균 mean
$\gamma:$ 분산 variance
위 이미지의 우측은 Normalization이 필요 없는 경우를 의미.
학습이 끝나고 $\gamma, \beta$가 저런 값이 나왔다면 normalization이 필요없다는 의미.
추가적으로, 최종 z값은 $z_{norm}$이 아니고 $\tilde{z}$ (tilde 붙은 것)
Adding Batch Norm to a network
batch norm은 보통 output layer를 제외한 레이어에 적용한다.(당연한 얘기겠지만 output결과를 바꾸니까)
W, b뿐만 아니라 $\gamma$ $\beta$ 도 업데이트 해야 함.
gradient decent 사용할 수 있음.
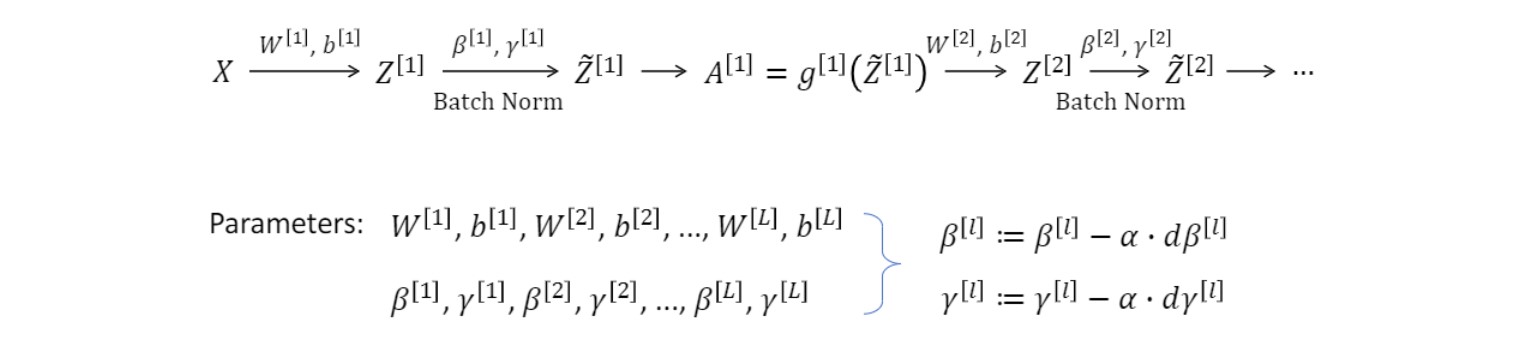
(실제로 굉장히 많이 쓰기 때문에 하단과 같이 제공됨) tf.nn.batch_normalization torch.nn.modules.batchnorm
Working with mini-batches
- $\gamma$와 $\beta$는 각 mini-batch에서 공유.
batch wise가 아닌 mini-batch 단위로 학습하는 경우,
평균이랑 분산 값도 각 mini-batch에서 구해야 함.(당연한 말임)
하지만 $\gamma$와 $\beta$는 각 mini-batch에서 공유.
(-> 이부분 살짝 헷갈렸었는데, W랑 b업데이트 하듯이 생각하면 됨. 결국 Weight도 순전파 mini-batch단위로 하지만 각 batch에서 공유되는 값이니까)
- trainable parameter w b $\gamma$ $\beta$ -> w $\gamma$ $\beta$

$\beta$와 b는 역할이 같음. 따라서 batch normalization 진행 시 b를 더할 필요 없음
shift mean이라는 같은 역할하기 때문
$\beta$가 아닌 b를 없앤 이유:
정규화 이후에 shift하고싶기 때문
feature normalization의 핵심은,
training! training 동안 $\beta$ $\gamma$ 를 찾는것!
- Why batch normalization work?
검은 고양이로 학습하고 노란 고양이사진에서 고양이 찾으라고 하면 찾기 어려울 것임.
-> covariate shift (= distribution mismatch)
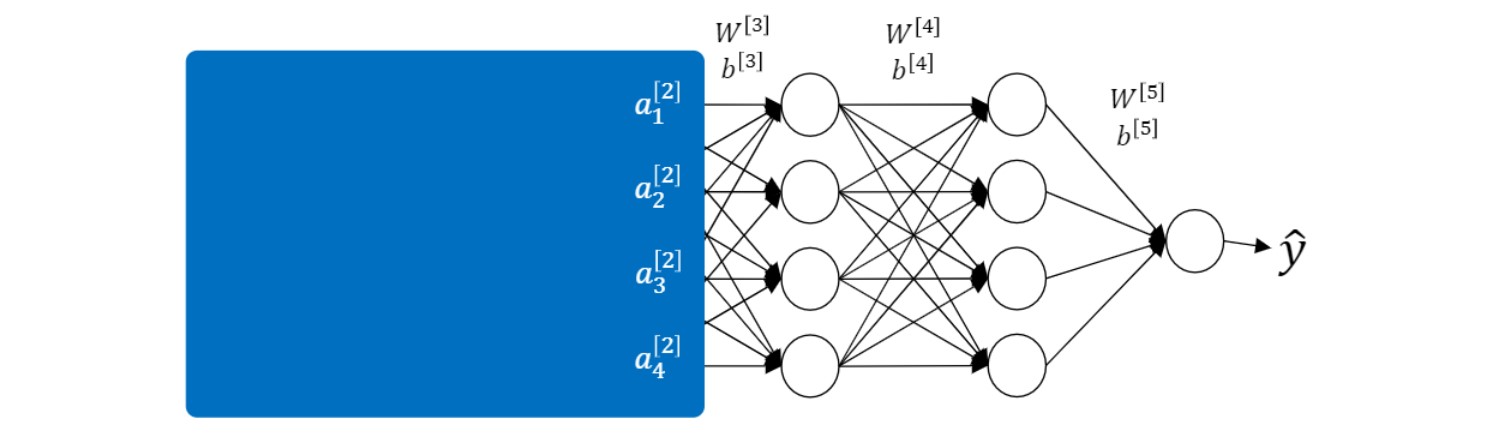
$W_3, W_4$를 업데이트 하는 경우,
파란색으로 가려진 부분의 $W_1, W_2$도 업데이트가 될 것이다.
따라서 $a_1, a_2, a_3, a_4$도 같은 이미지를 넣은 경우에도 값이 바뀌게 된다.
바뀌기 전 $a_1, a_2, a_3, a_4$ 값을 생각하고 업데이트 한 것인데 이렇게 되면 문제가 됨.
만약 batch norm 진행한다면 zero mean, 1 variance들어오게 되어 위의 문제 좀 해결할 수 있음
- batch norm at test time
test stage에서는 single image일 수 있다. 이 경우 batch normalization이 제대로 되지 않는 문제가 발생한다. 따라서 training때의 평균과 분산 가져와서 normalize 한다.
출처 : 2023-1 ITE4052 수업