Dynamic Programming

: 알고리즘의 한 종류.
(메모리를 좀 더 쓰고 대신 시간 절약하는 방법중 하나)
계산 결과를 저장해 두었다가 추후에 다시 사용.
DP라는 이름과의 연관성 낮음

큰 문제를 작은 문제로 나눠 푸는 것.
divide conquer와 비슷. 다만 작은 문제의 중복 유무가 큰 차이
dynamic programming은 작은 문제들이 반복 O

Contents
➖ Assembly-line scheduling
➖ Rod cutting
☑️ Longest common subsequence
➖ Matrix-chain multiplication

Longest common subsequence

문제 정의

최장 공통 부분 문자열

  • substring : 연속된 부분 문자열
    ex) CBD는 ABCBDAB 의 substring
  • subsequence : 연속적이지는 않은 부분 문자열
    ex) BCDB는 ABCBDAB 의 subsequence

2개의 string을 비교,

  • common subsequence BCA는 X=ABCBDAB와 Y=BDCABA 의 common subsequence

  • longest common subsequence (LCS)

X = A B C B D A B
Y = B D C A B A

위의 경우, X와 Y의 longest common subsequence는 BCBA

Brute force approach

  • X의 모든 subsequence 경우의 수가 Y의 subsequence인지 하나씩 확인 후 그 중 가장 긴 것 선택
  • 불가: X의 subsequence개수는 $2^m$개

Dynamic programming

정의

X의 $i$째 prefix $X_i$는, $X_i=x_1,x_2 … x_i$

만약 X = ABCB라면,

  • $X_4$ = ABCB
  • $X_0$ =

1: $x_m=y_n$이면, $z_k=x_m=y_n$. 그리고 $Z_k-1$ 은 $X_{m-1}$과$Y_{n-1}$의 LCS

X = A B C B D A B
Y = B> D C A B

2: $x_m\neq y_n$이면, Z는 $X_{m-1}$과 $Y$ 혹은 $X$와 $Y_{n-1}$의 LCS이다.

C[i][j]는 sequence $X_i$와 $Y_j$의 LCS

1

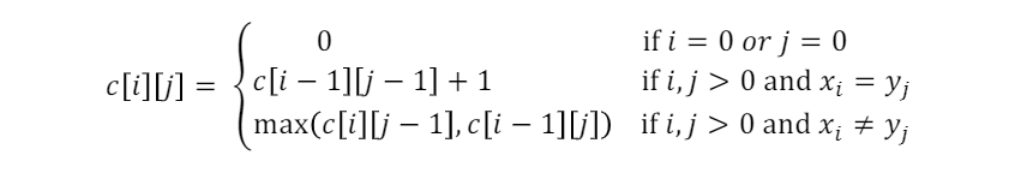
i=0 또는 j=0인 경우 0,
$x_m, y_n$ 같다면 이전 CLS 길이에 +1,
다르다면 위($c[i-1][j]$)와 왼쪽($c[i][j-1]$)값 중 큰값이 오게 된다.

2

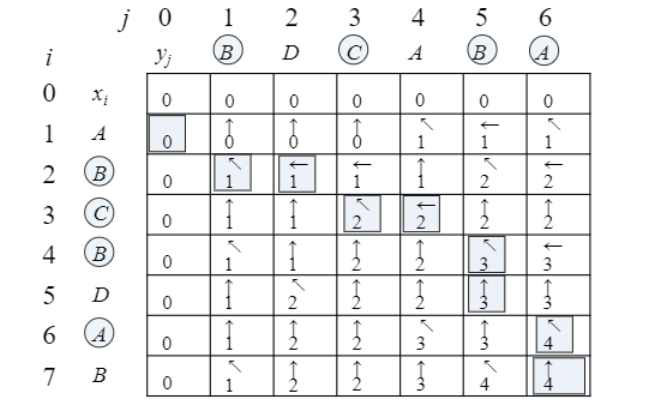
multiple LSCs

3

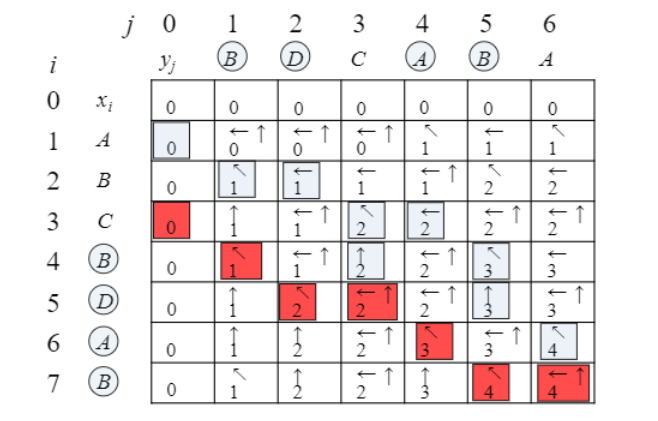
위의 표와 같이 여러 경로를 통해 같은길이의 LCS가 여럿 나올 수 있다.

pseudo code

LCS-LENGTH (X, Y)
    m = X.length
    n = Y.length
    let b[1 .. m][1 .. n] and c[0 .. m][0 .. n] be new tables
    for i= 1 to m 
        c[i][0] = 0
    for j= 0 to n
        c[0][j] = 0 
    for i= 1 to m
        for j= 1 to n
            if xi== yj
                c[i][j] = c[i−1][j−1] +1
                b[i][j] = "↖"
            elseif c[i−1][j] ≥ c[i][j−1]
                c[i][j] = c[i−1][j]
                b[i][j] = "↑"
            else c[i][j] = c[i][j−1]
                b[i][j] = "←"
                return c and b

PRINT-LCS (b, X, i,j)
    if i==0 or j==0
        return 
    if b[i][j] =="↖"
        PRINT-LCS (b, X, i−1, j−1)
        print xi
    elseif b[i][j] =="↑"
        PRINT-LCS (b, X, i−1, j)
    else PRINT-LCS (b, X, i, j−1)

space consumption

$\theta(mn)$

time consumption

$\theta(mn)$

space reduction

$\theta(min(m,n))$
(LCS length only)

  Space Time
Assembly-line scheduling $\theta(n)$ $\theta(n)$
Rod cutting $\theta(n)$ $\theta(n^2)$
Longest common subsequence $\theta(mn)$</br>$\theta(n^2)$ $\theta(mn)$</br>$\theta(n^2)$
Matrix-chain multiplication    

출처 : 2023-2 ITE2039 수업

https://twinw.tistory.com/126