Amortized Analysis

이전까지 operation의 asymptotic boundary 구했음. (e.g. sort 비교횟수-> boundary)

이 chapter에서는, push-pop 할때 push와 pop 수행시간 각각 구해서 합하는게 아닌, push, pop 합해서 n번 발생했을 때 전체 cost 구하는 것.

= 독립적으로 시간복잡도 구하는 것이 아닌, 여러 operation의 시퀀스 한꺼번에 시간복잡도 분석.

(최악의 경우를 과하게 잡지 않도록)

특정 일을 할 때 100번 진행하는 경우 99번 1분이 걸리고, 1번정도 10분이 걸린다. 이때 최악의 경우 10분으로 잡고 이 일을 반복하는 횟수를 곱하게 되면 너무 과하게 upper bound를 잡는다는 것에서 시작.
각 시퀀스의 upper bound를 구하고 이를 진행 횟수만큼 곱하는 것이 아닌 한번 진행할 때에 대한 평균적 시간을 구해서 upper bound를 구하자.
n회 진행 시 총 걸리는 시간 T(n)을 구할 수 있다면 T(n)/n이 한번 진행시 걸리는 시간이고, 이것이 한번 진행했을 때 최악의 시간(위 예시에서 10분) 보다 짧다면 평가절하를 줄인것.

amortized 예시
참고

Contents

➖ Aggregation analysis
➖ Accounting method
☑️ Potential method
➖ Dynamic Table

Potential method

Amortized analysis의 수행시간 분석하는 세번째 방법

물리에서 봤던 퍼텐셜에너지(=위치에너지)의 그 potential

  • 자료구조의 specific object가 아닌 자료구조 전체를 “potential“이라고 봄.

13

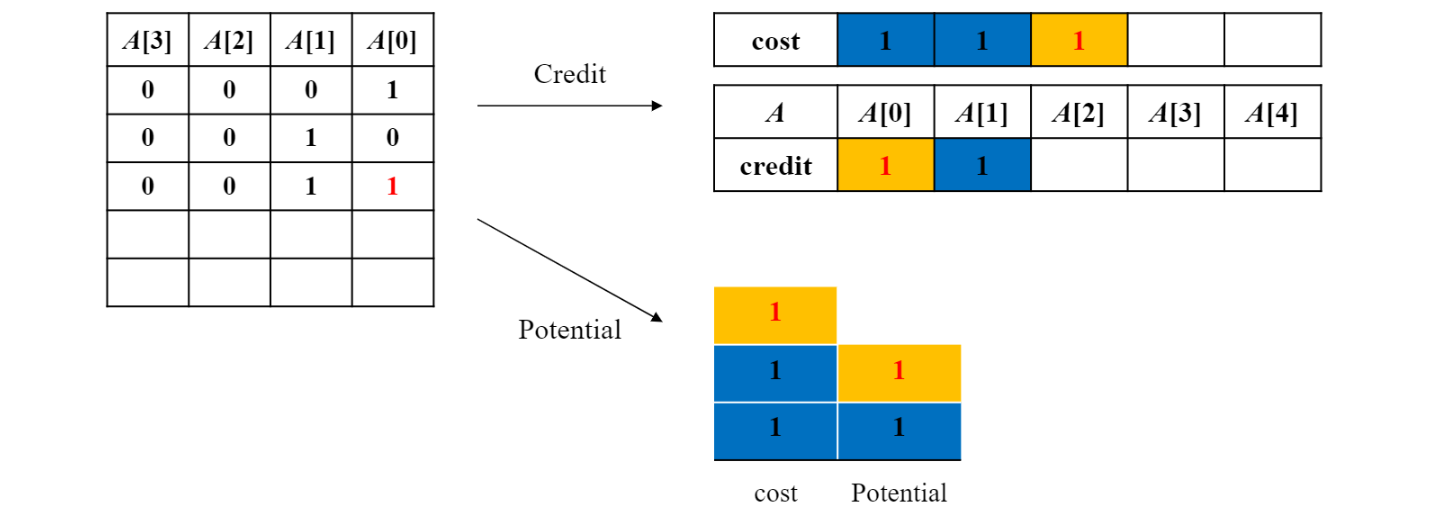
credit 보던 accounting method와 유사.

  • bit 전체의 credit 보겠다는 의미.
    -> bit 전체에 있는 1의 개수



  • n번의 operation 수행 시,
    $D_0$ : 초기 자료구조 (data structure)
    $D_i$ : $D_{i-1}$에 i번째 operation수행 후 자료구조의 결과
    $\Phi(D_i)$ : 자료구조 $D_i$와 관련된 potential

  • Potential difference ($\Phi(D_i)-\Phi(D_{i-1})$)
    i번째, i-1번째 potential의 차이
    • positive
      자료구조의 potential이 증가
    • negative
      자료구조의 potential이 감소
      실제 cost를 potential이 pay
  • Amortized cost
    $\hat{c_i}=c_i+\Phi(D_i)-\Phi(D_{i-1})$
    • $c_i$: actual cost,
    • $\Phi(D_i)-\Phi(D_{i-1})$: potential difference
  • n operation의 total amortized cost $\sum_{i=1}^n\hat{c_i}=\sum_{i=1}^n(c_i+\Phi(D_i)-\Phi(D_{i-1}))$
    $=\sum_{i=1}^nc_i+\Phi(D_n)-\Phi(D_0)$
    D 맨앞, 맨뒤만 남음

$\therefore$ $\sum_{i=1}^n\hat{c_i}\geq\sum_{i=1}^n{c_i}$   ($1\leq k\leq n$) 이 조건 만족 위해,
모든 i에 대해, $\Phi(D_i) \geq \Phi(D_0)$ 이 조건 만족 해야함.

예시1: Stack operation

  • Potential function $\Phi$
    stack에 들어있는 object의 # 라고 하면,
    $\Phi(D_0)=0$
  • i번째 operation 수행 후 stack인 $D_i$는 nonnegative potential
    • $\Phi(D_i)\geq0$ $=\Phi(D_0)$
  • 각 operation의 amortized cost
    • PUSH operation

      i번째 operation이 PUSH이고 stack에 (operation 전) s개의 object 포함하고있다면,

      • $\Phi(D_i)-\Phi(D_{i-1})$ $= (s+1)-s=1$
      • amortized cost는, $\hat{c_i}=c_i+\Phi(D_i)-\Phi(D_{i-1})$
                                        $=1+(s+1)-s $
                                        $=2$
    • POP operation

      i번째 operation이 POP이고 stack에 s개의 object 포함하고있다면, (+empty 아닌경우)

      • $\Phi(D_i)-\Phi(D_{i-1})= (s-1)-s=-1$
      • amortized cost는, $\hat{c_i}=c_i+\Phi(D_i)-\Phi(D_{i-1})$
                                        $=1+(s-1)-s $
                                        $=0$
    • MULTIPOP(S,k) operation

      i번째 operation이 MULTIPOP이고 stack에 s개의 object 포함하고있다면,

      • $k’=min(k,s)$ : stack에서 pop할 object의 수
        $\Phi(D_i)-\Phi(D_{i-1})=-min(k,s)=-k’$
      • amortized cost는, $\hat{c_i}=c_i+\Phi(D_i)-\Phi(D_{i-1})$
                                        $=k’-k’ $
                                        $=0$

  • Amortized cost : $O(1)$

  • Total amortized cost : $O(n)$

  • Total actual cost : $O(n)$

예시2: Binary counter

  • Potential function $\Phi$
    array에 있는 1의 #
    • $b_i$ : $i$번째 INCREMENT operation 이후 counter에 있는 1의 #
    • $t_i$ : $i$번째 INCREMENT operation 에서 reset되는 bit의 #
  • $i$번째 operation의 actual cost
    • $c_i\leq t_i+1$
INCREMENT (A)
    i= 0
    while i < A.length and A[i]  ==  1
        A[i]  =  0
        i=  i+  1
    if i < A.length
        A[i]  =  1




  • $b_i=0$인 경우,
    • 다 1로 차있어서 전부 0으로 reset되는 상황
    • $b_i=t_i=k$ 14
  • $b_i>0$인 경우,
    • $b_i=b_{i-1}-t_i+1$ 15

      추가 예시
      10011 -> $b_{i-1}=3$
      10100 -> $b_{i}=2$
      $t_i=2$ (bit 2개 reset)
      $b_i=b_{i-1}-t_i+1=3-2+1=2$

=> 위 두가지 모두
$b_i\leq b_{i-1}-t_i+1$만족




  • Potential difference
    • $\Phi(D_i)-\Phi(D_{i-1})= b_i-b_{i-1}$
                                        $\leq (b_{i-1}-t_i+1)-b_{i-1} $
                                        $=1-t_i$
  • Amortized cost
    • $\hat{c_i}=c_i + \Phi(D_i)-\Phi(D_{i-1})$
           $\leq (t_i+1)+(1-t_i)=2$
      -> $O(1)$




  • Counter가 zero에서 시작한다면
    $\Phi(D_0)=0$ and $\Phi(D_i)\geq 0$가 모든 $i$에 대해 성립
    • n회의 INCREMENT operation의
      총 amortized cost는 실제 총 cost의 upper bound
    • n회의 INCREMENToperation의 worst-case cost는 $O(n)$
  • Counter가 zero에서 시작하지 않는다면
    $0\leq b_0, b_n\leq k$ (이때 k는 counter의 bit 수)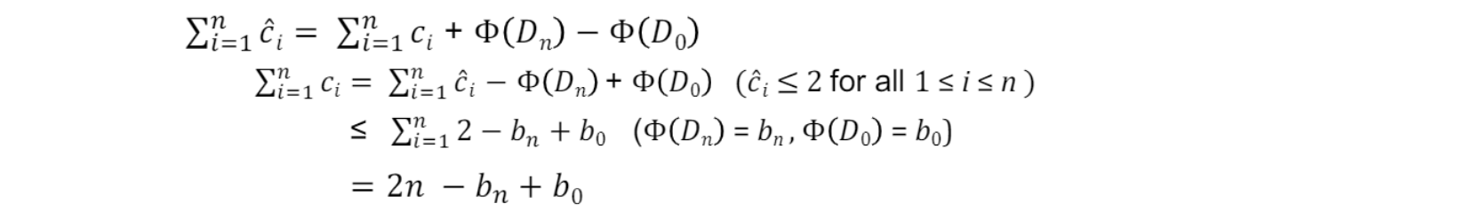 16 $\therefore$ total actual cost는 $O(n)$

출처 : 2023-2 ITE2039 수업