Eye-Camera Analogy

computer vision의 basic idea.
Computer를 사용해 vision(human vision system)

image?

: 8bit의 integer matrix
각 숫자는 how strong the light is($\therefore$　0-> 검, 255-> 흰)

Pinhole Camera

Camera Anatomy

1

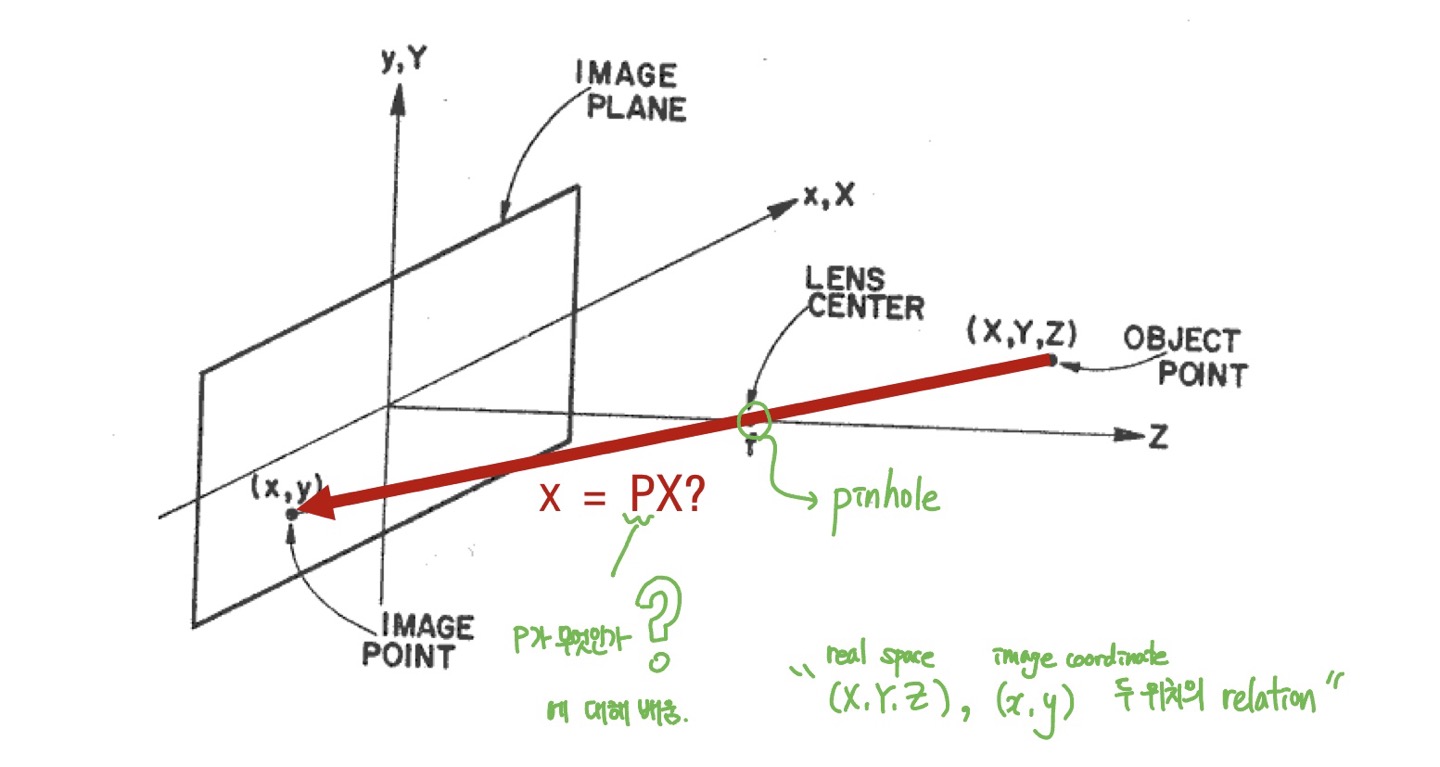
3D -> 2D 변환 위해서 행렬 P에 무엇이 들어가야 하는가?에 대한 것

«  3D 이전에 2D에 대한 transformation 먼저!  »

2D image transform

Affine transformation 3가지

  1. Translation
  2. Scaling
  3. Rotation

2

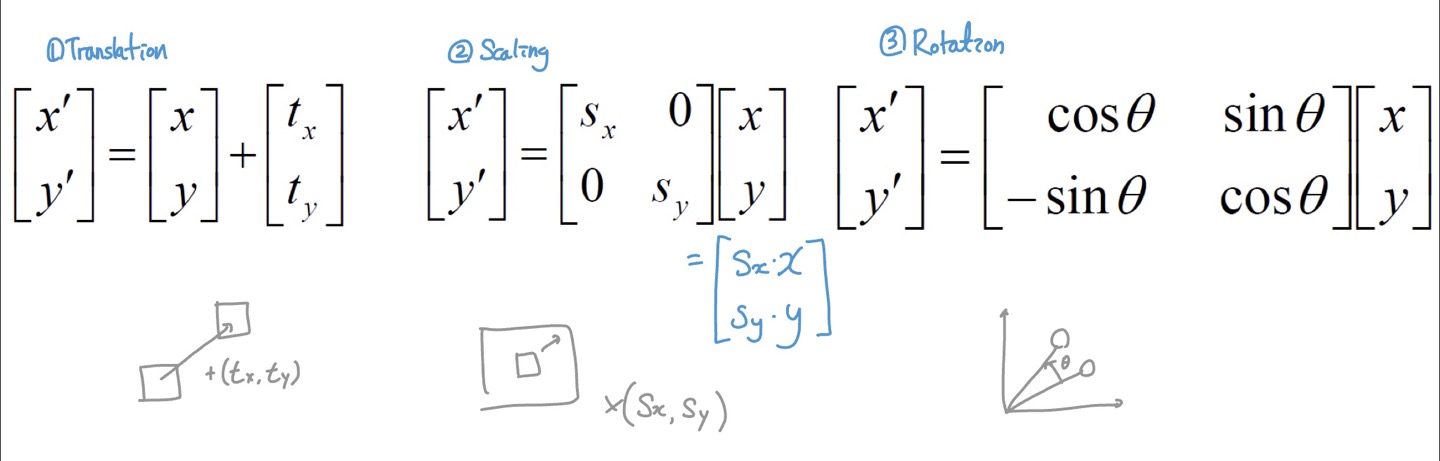
Linear Transformations

  • Scaling　　$S(s_x,s_y) = \begin{bmatrix}s_x&0 \ 0&s_y \ \end{bmatrix}$

    • inverse : $S$( $1\over{s_x},$ $1\over{s_y}$)

  • Rotation　　$R(\theta) = \begin{bmatrix}cos\theta&-sin\theta \ sin\theta&cos\theta \ \end{bmatrix}$

    • inverse : rotation은 $R^{-1} = R^T$
      $R(-\theta) = \begin{bmatrix}cos\theta&-sin\theta\ sin\theta&cos\theta\ \end{bmatrix} = R^T$
      rotation matrix는 inverse = transpose인 unitarymatrix

  • Mirror　　$T = \begin{bmatrix} -1&0 \ 0&1 \ \end{bmatrix}$　　y축 대칭
    　　　　 $T = \begin{bmatrix}1&0\0&-1\ \end{bmatrix}$　　x축 대칭

하지만 **Translation is not a linear operation on 2D coordinates!!**

linear function의 정의

  1. $f(ax) = af(x)$
  2. $f(x+y) = f(x) + f(y)$

2D translation은 이를 만족시키지 않는다.

Homogeneous Coordinates

3

translation까지 matrix multiplication으로 표현하고 싶어서 고안한 방법

Affine transformations

: 마지막 줄이 [0 0 1]인 3x3 matrix

$T = \begin{bmatrix}a&b&c \ d&e&f \ 0&0&1 \ \end{bmatrix}$

맨 아랫줄이 ‘0 0 1’이 되는 matrix 모두 affine이므로,
translate, scale, 2D rotation 모두 포함

Projective transformations (Homography)

4

$H = \begin{bmatrix}a&b&c \ d&e&f \ g&h&1 \ \end{bmatrix}$

5

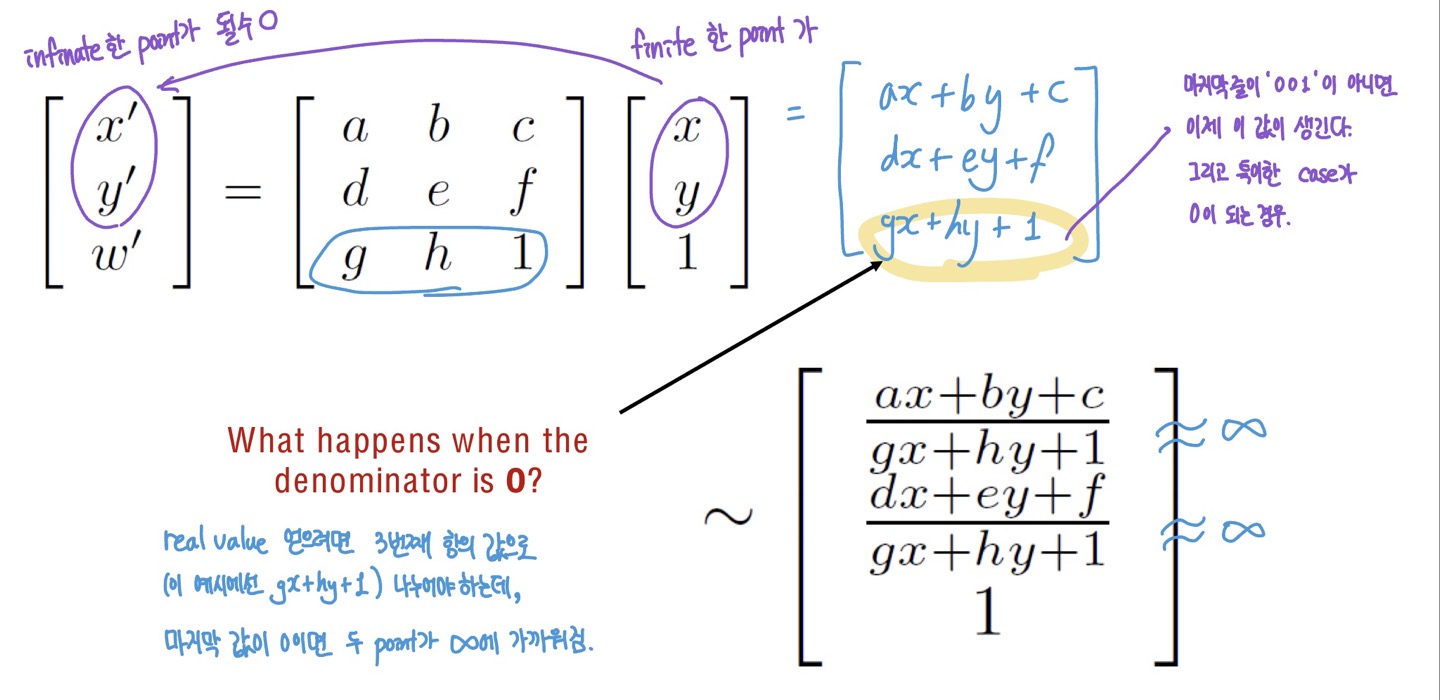
Points at Infinity

6

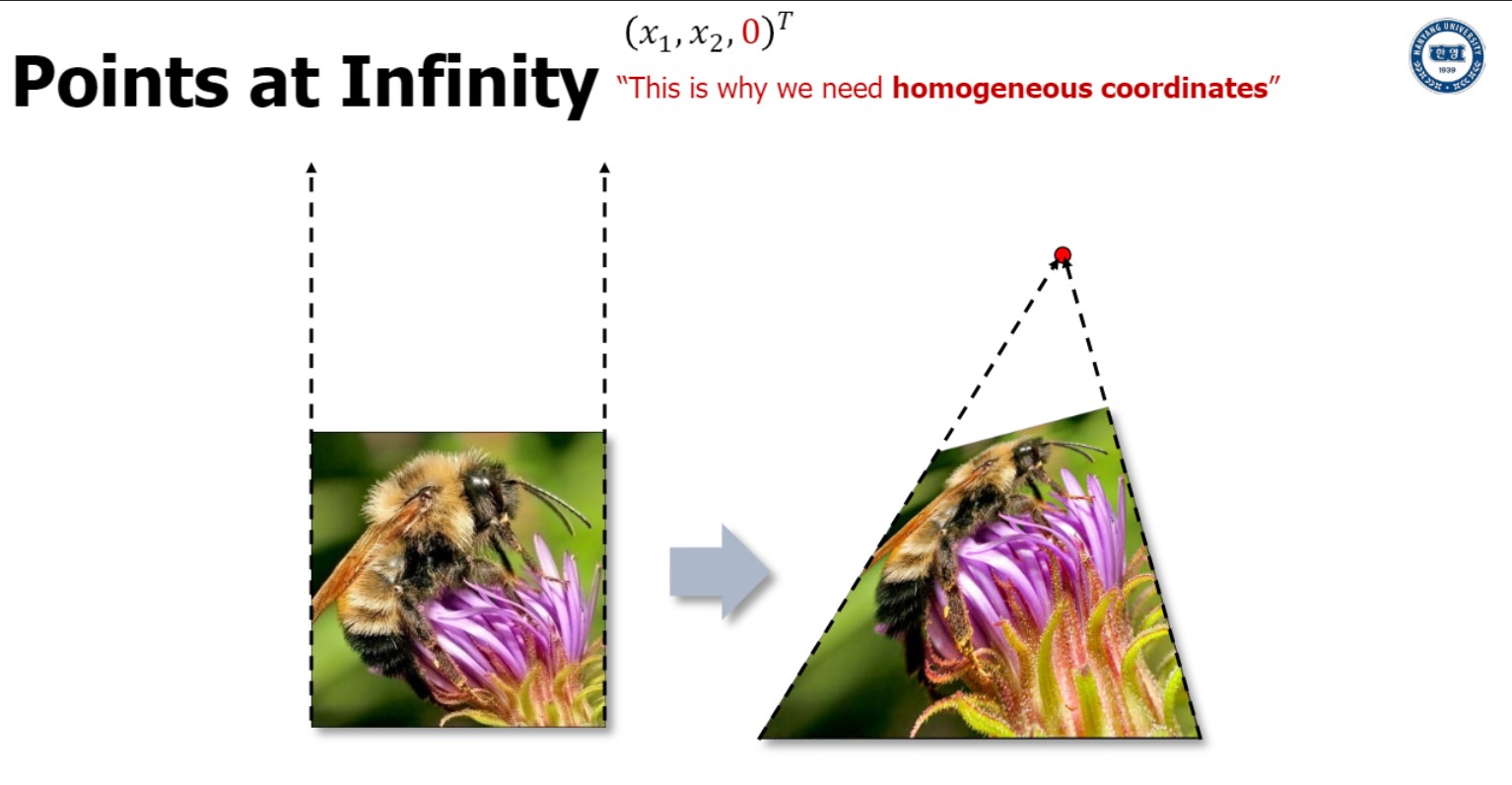
$(x_1,x_2,0)$에서 마지막 자리를 0으로 만들면 이것을 1로 만들기 위해 앞부분이 infinite해지게 됨.
-> 이것이 homogeneous coordinate가 필요한 이유

Removing Projective Distortion

7

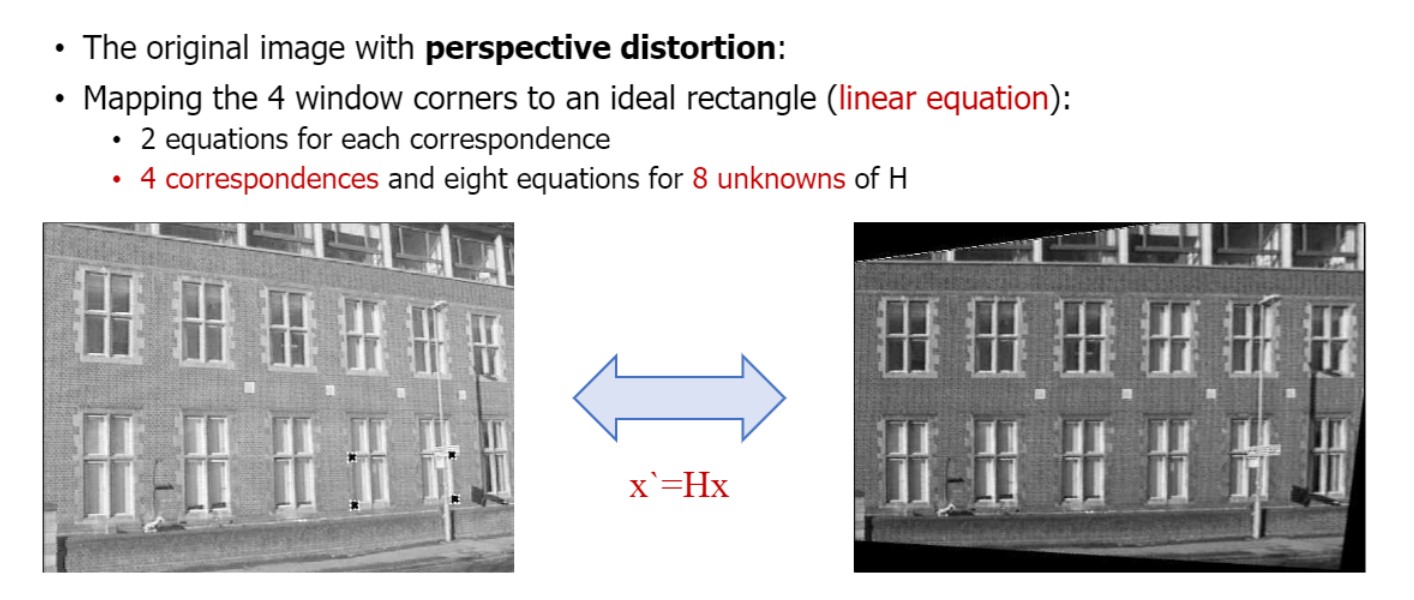
rectify image 바로잡는 방법 = 대응하는 point 찾기

homography matrix의 unknown의 개수는 8개.

각 corresponding에는 equation 2개씩 있다.
($\because$ x,y 있다면 한 점에 2 equation)

따라서 8개의 unknown 찾으려면 4개의 corresponding으로 가능

2D Image Transformations ⭐

8

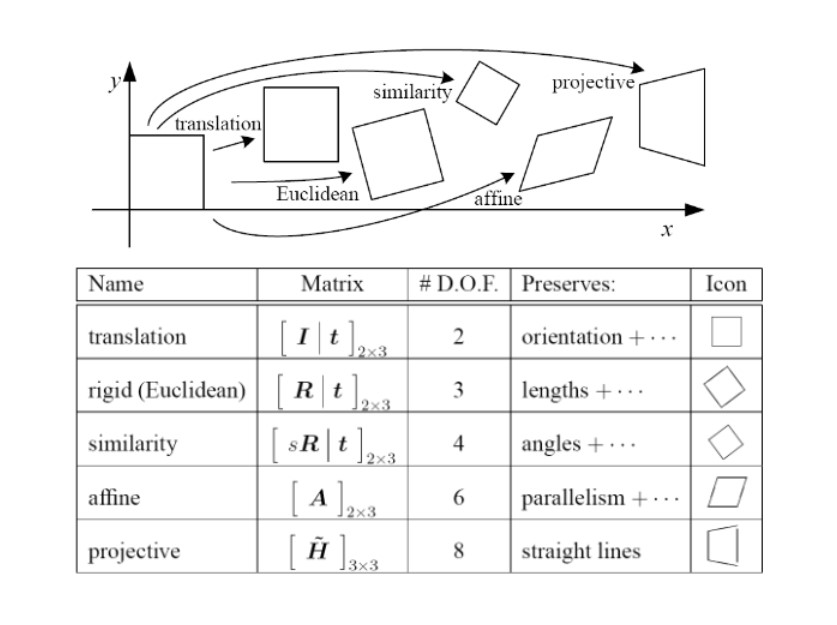
3D transformation

변수 하나 추가된 것.

다만, rotation은 주의.

< rotaton 수식 첨부>

19

Perspective Projection Model

camera가
world 좌표계의 X, Y, Z(3D) -> camera 좌표계의 x, y(2D)

9

카메라 pinhole이 원점에 맞춰져있고, 이미지 plane이 x y z에 맞춰져 있는 이상적인 경우

offset이 있는 경우

10

11

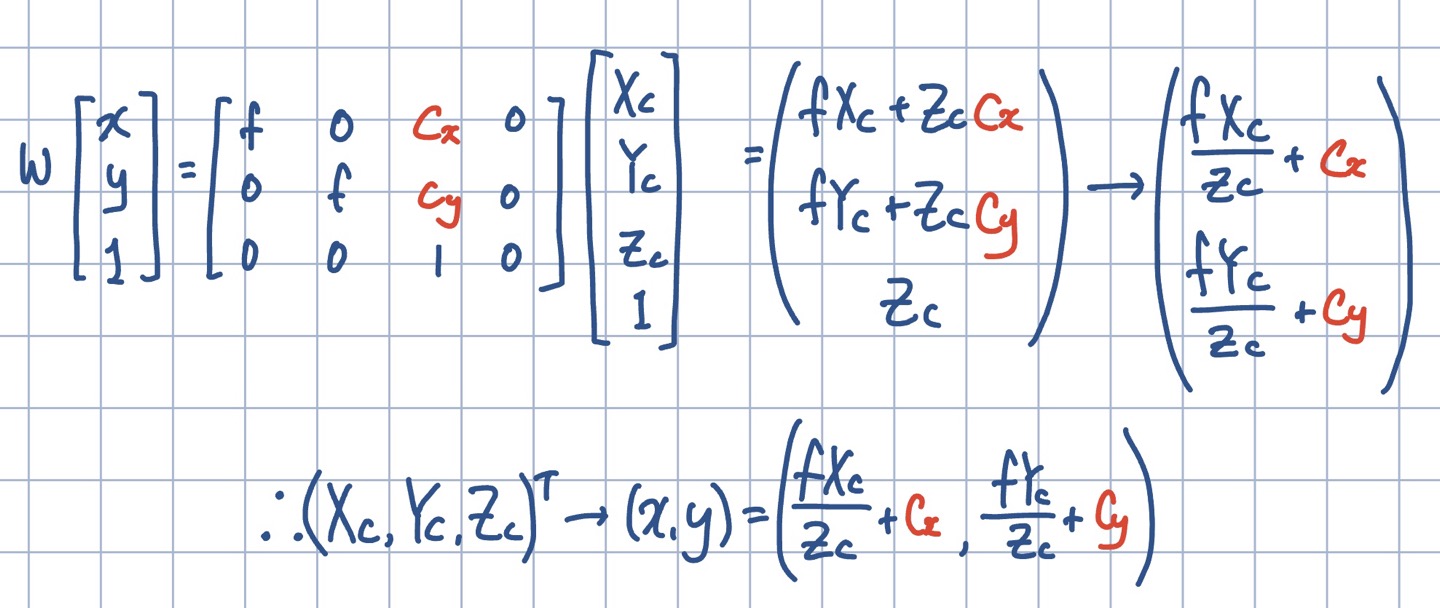
=> 하나의 카메라 내부에서 일어나는 일을 표현하는 것이기 때문에 “Intrinsic Parameter” 라고 한다.

(카메라 간의 관계를 표현하는 것은 Extrinsic parameter)

Camera Rotation and Translation

world 좌표계에서 camera 좌표계변환 위해 transformation

12

13

14

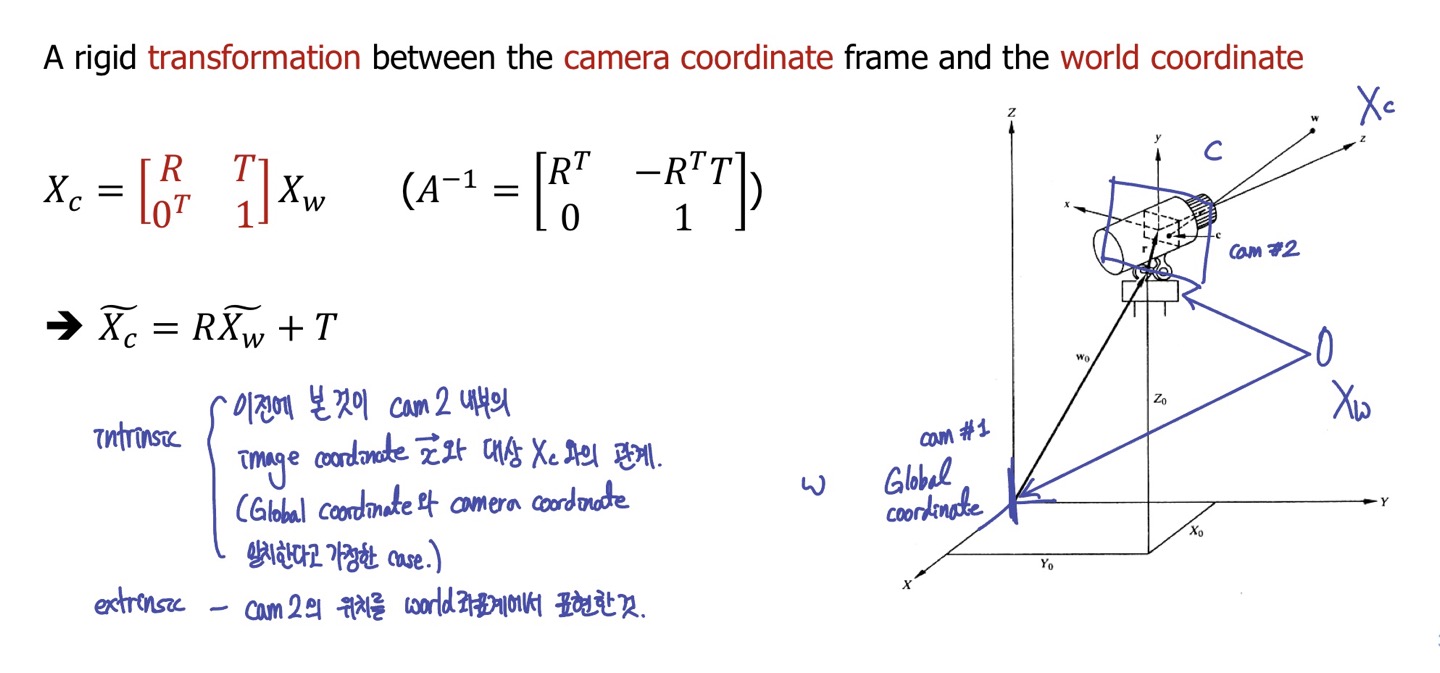
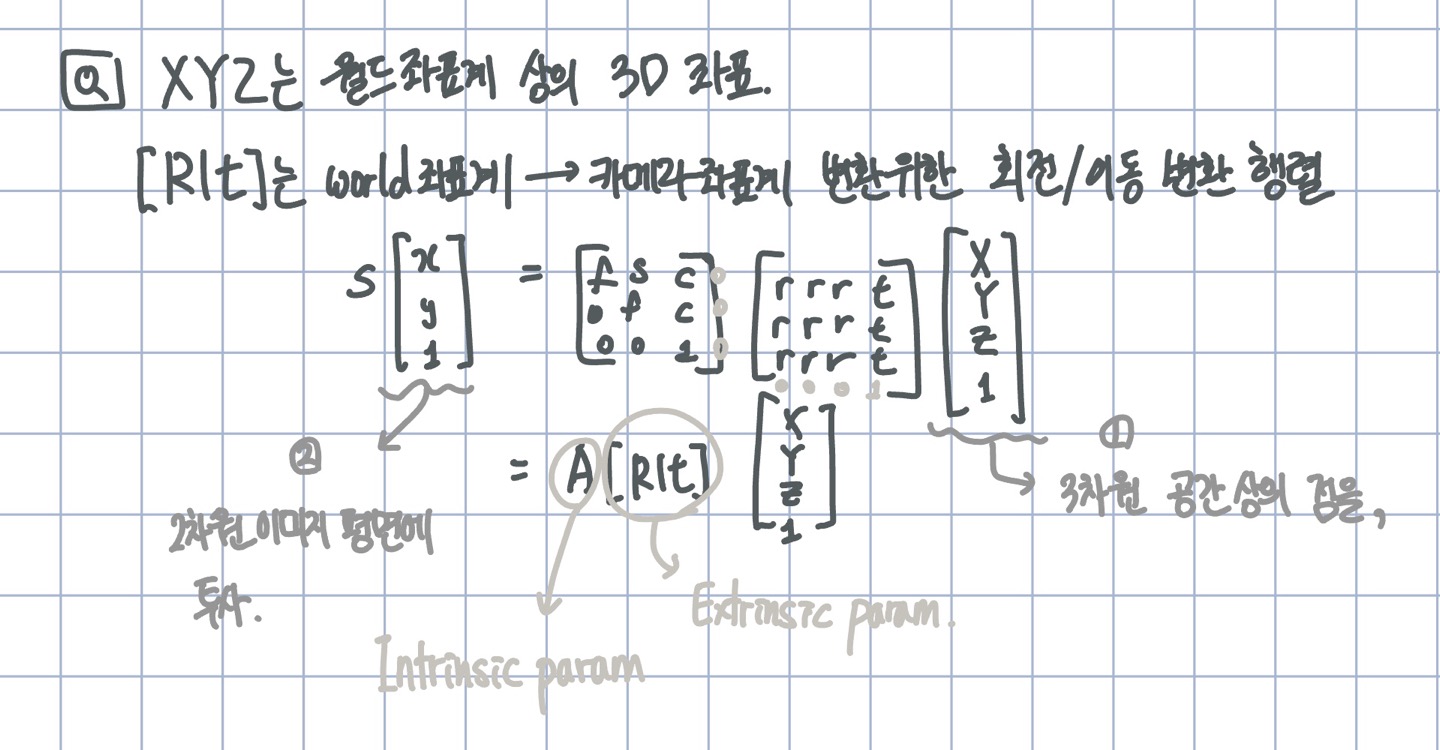
Camera calibration :
camera paramete들 얻기 위한 것. (linear equation)

⭐
\(\overrightarrow{x} = K[I|0] \overrightarrow{X_c} \Rightarrow K[R|t] \overrightarrow{X_w}\)

#

Q. 3D->2D 했는데, 역으로 가능한가?
A. No. 2D-> 3D 완벽히 불가

InversePerspective Transformation

15

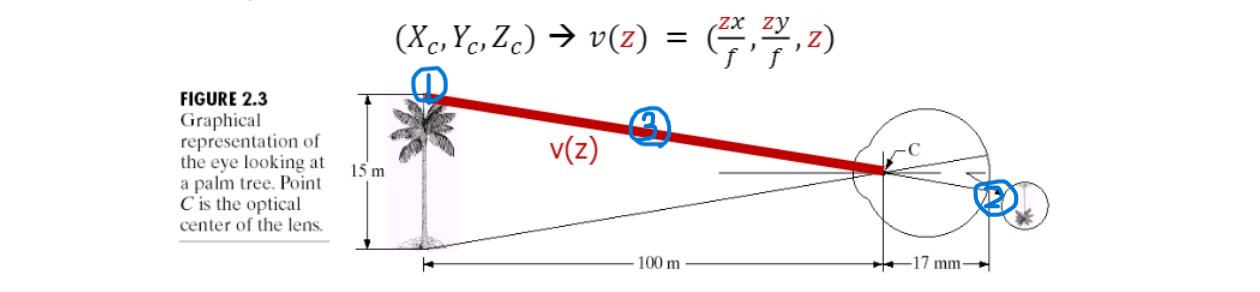
이미지에서 1은 2에 상이 맺힌다.
하지만 3위치 또한 2에 상이 맺힌다.
$\therefore$ 2에 위치한 상을 3D에 완벽하게 표현이 불가하다.
(depth 정보 X)

reconstruct 하려면 2개 이상의 뷰가 필요하다.
-> stereo vision

Single Image Depth Estimation

: single image(2D)만 가지고 완벽히 3D복원 불가능.
but, 사람은 2D 이미지로 depth 추측한다(이전에 본 착시 처럼)
사람이 경험을 토대로 추측하듯 딥러닝도 학습해서 estimate 할 수 있게.

  • single RGB image로 depth 정보 추측
  • geometric 정보의 부족 -> ill-posed problem
  • Deep learning으로 data에 기반해서 모델이 depth guess 하도록 함

From Pinhole to Real Cameras

pinhole카메라와 실제 카메라의 차이

구멍의 크기가 0인 pinhole카메라와 달리 실제 카메라는 큰 크기의 렌즈를 가지고있다.
-> 각 point에 single ray가 닿지 않고 톡정 범위의 빛이 이미지의 한 점에 도달하게 된다.
=> Blurring 발생

따라서 실제 카메라에서는 조리개 값 조절해야함.

F-Number

: 조리개값 (f# = f/d)

  • 이미지의 밝기를 조정한다.
  • depth of field에 영향을 줌
  • (밝기와 depth of field는 trade off 관계)

d와 f# 반비례 관계.

  • Small f# -> big apature(조리개 d)
  • Large f# -> small apature

16

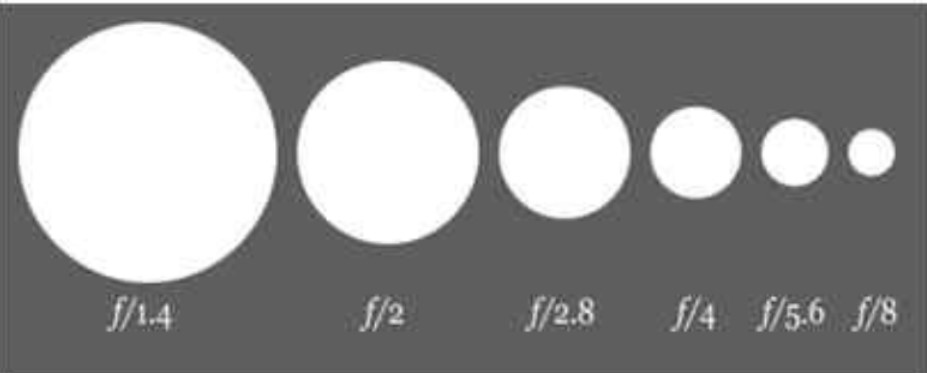
Depth of Field and Apature

Depth of Field (피사계심도)

  • 이미지에서 선명하게(sharp) 나온 범위
  • f-number(apature)에 의해 결정
    .
  • Small f# -> big apature(조리개 d) -> narrow depth of field
  • Large f# -> small apature -> broad depth of field

f# $\Downarrow$ -> apature(조리개) $\Uparrow$ -> depth of field $\Downarrow$
f# $\Uparrow$ -> apature(조리개) $\Downarrow$ -> depth of field $\Uparrow$

17

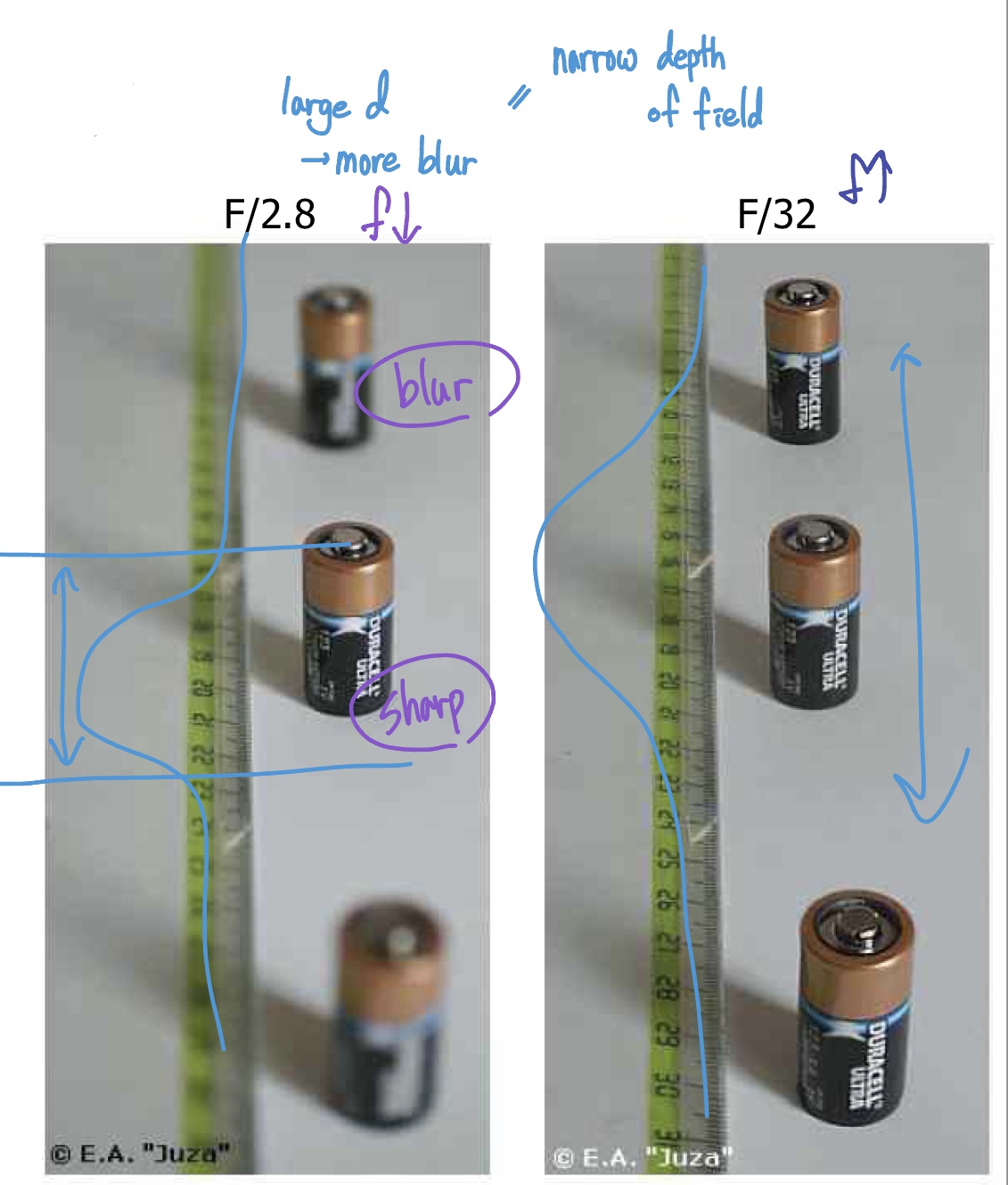
Brightness of Images

이미지 밝기에 영향 주는 것들

1) Apature

: 센서에 떨어지는 빛의 양에 따라 밝기 결정

  • Small f# -> big apature(조리개 d) -> narrow depth of field
  • Large f# -> small apature -> broad depth of field

f# $\Downarrow$ -> apature(조리개) $\Uparrow$ -> I $\Uparrow$(bright)
f# $\Uparrow$ -> apature(조리개) $\Downarrow$ -> I $\Downarrow$(dark)

$I \propto \frac{1}{(f#_)^{2}} \propto A$

밝은것과 blurry -> trade off 관계

2) ISO Gain, 3) Shutter speed

: 센서 파라미터들에 의해 밝기 영향 받음

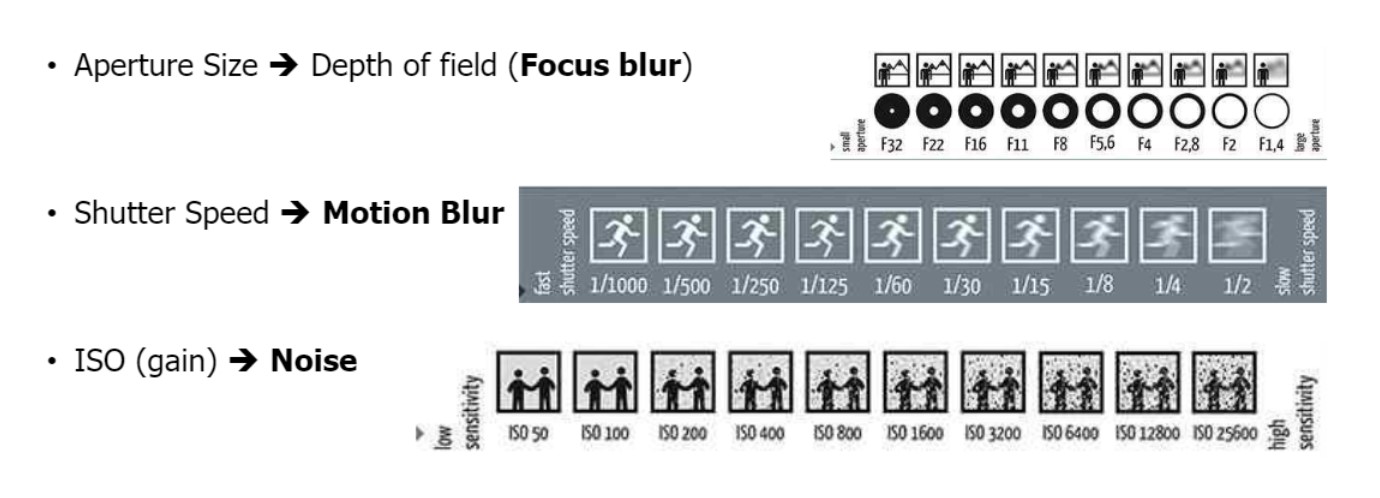
Image Quality Control

위 밝기 조절 3가지 방법들은 각자 trade off 있음 ⭐

  1. Apature size $\Uparrow$ : defocus blur
  2. Shutter speed $\Downarrow$ : motion blur
  3. larger ISO gain : noise

18

복습

2D, 3D의 각 transformation들의 행렬과 DOF?

Single Image Depth Estimation의 아이디어?

이미지의 밝기에 영향을 주는 것 3가지와 각 방법의 trade off는?

출처 : 2023-1 ITE4052 수업
출처2