Merge Sort

: sort 된 두 key들의 list로 하나의 정렬된 list를 만드는 merge를 사용한 sorting 알고리즘

Pseudo Code

아래 pseudo code에서 의미하는 p, q, r :
(전체 array가 A)

1


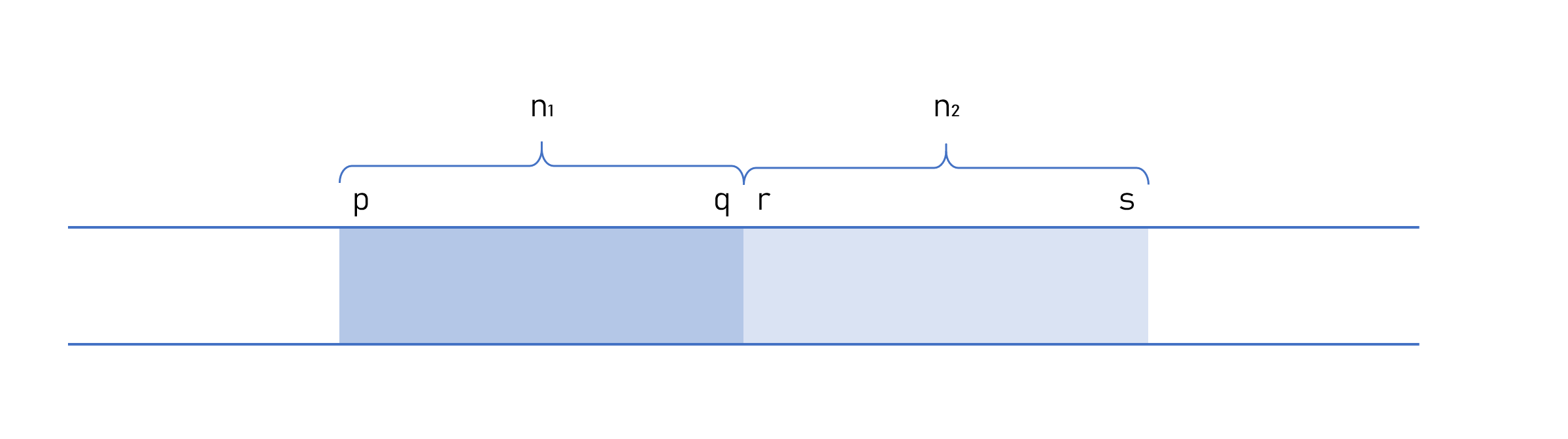
MERGE(A,p,q,r){
    n1 = q-p+1
    n2 = r-q
    let L[1..n1+1] and R[1..n2+1]
    for i=1 to n1
        L[i] = A[p+i-1]     // 배열 A의 좌측 값들을 새로운 배열 L로 복사
    for j=1 to n2
        R[j] = A[q+j]     // 배열 A의 우측 값들을 새로운 배열 R로 복사
    L[n1+1] = ∞     //  ∞ : 이 array에 나오지 않을 숫자
    R[n2+1] = ∞     // 한쪽 끝나면 ∞ (무한)이라 표시한 sentinel value와 비교
    i = 1
    j = 1
    for k=p to r
        if L[i] <= R[j]
            A[k] = L[i]
            i ++
        else
            A[k] = R[j]
            j ++
}

Merge의 running time

n1, n2가 정렬된 두 list의 길이라면,
main operation이 compare & move.

이때 # of compare   $\le$   # of move
(이동 하는 횟수가 비교하는 횟수보다 많거나 같다)

$\therefore$ movement #   =   $n_1 + n_2$ 이므로,
comparison # + movement #     $\le$   $2(n_1 + n_2)$

$\theta(n_1 + n_2)$

divide-and-conquer approach

  • Divide : n개의 key를 n/2 key 씩 2개로 분할
  • Conquer : 재귀적(recursively)으로 merge sort 사용해 정렬
  • Combine : 두 sorted list merge

Pseudo Code


MERGE-SORT(A,p,r){
    if p < r
        q = ⌊(p+r)/2⌋
        MERGE-SORT(A,p,q)
        MERGE-SORT(A,q+1,r)
        MERGE(A,p,q,r)
}

Running time

  • Divide: $\theta(1)$
    $\because$ Array의 중앙만 연산

  • Conquer : $2\times T(n/2)$
    두개의 sub set 재귀적으로.
    각 부분문제는 크기가 $n/2$

  • Merge : $\theta(n)$
    (위에서 이미 보임)

$T(n) = \begin{cases} \theta(1) & \text{if }n=1 \ 2T(n/2)+\theta(n) & \text{if }\ge 1 \end{cases}$

       $\downarrow$

$T(n) = \begin{cases} c \ 2T(n/2)+cn \end{cases}$

nlgn

2
각 레벨마다 cn씩 lg(n+1)개의 레벨
-> cn(lg(n+1))

추가 설명
배열 길이 $N=2^k$라 할때 합병 단계는 k회 발생
(한번의 합병 단계엔 여러번의 합병 발생
한번의 합병 일어날 때 마다 임시 배열 원소 정렬 하면서 원소 개수만큼 비교 연산)
각 단계 에서 $2N$만큼의 이동, 비교 연산 일어남.
$\therefore$(합병단계 k회) x (각 단계에서 연산 횟수 $2N$)
$=O(kN)$
$N=2^k$, $k=logN$이므로, $O(kN) = O(NlogN)$

※레벨 수 주의
n=1일 떄 한 레벨인데 $lg1=0$이므로,
$lg(n+1)$이 올바른 레벨 수

출처 : 2023-2 ITE2039 수업