ITE4053_DL > 07-1 Problem Settings
Dataset, train dev test set, bias and variance, regularization
목차
- Problem Setup
- Bias/Variance
- Tips
Problem Setup
Applied ML is a highly iterative process
- NN 학습시, 많은 결정을 내려야 한다:
- 레이어의 수
- hidden unit의 수
- learning rate
- activation function 등
-
한번에 hyperparameter들에 맞는 값을 찾는 것은 거의 불가능하다.
- 따라서 machine learning은 매우 반복적인 작업.
Dataset
: 모델 만들 때 데이터 나누어 사용
-
- Traning sets
- unknown 변수 update 하는데 사용
- (지금까지는 trainset만 가지고 이야기 했음)
-
- development sets
- evaluate(잘하고 있다, 아니다 평가용도) –?
- test sets
결과에 매우 중요
Train/Dev/Testset
” 어떻게 나눌 것인가 하는 문제 “
rule of thumb for splitting data
- previous era (# of samples = 100 or 1000 or 10000)
training/test = 70/30 % training/dev/test = 60/20/20 % - big data era /(# of samples = 1,000,000) : 양 많은 경우
training/dev = 99/1 %
-> 데이터셋 양이 적은 경우 test set 비율 ⬆️
-> 데이터셋 양이 많다면 test set 비율 ⬇️
K-Fold Cross-Validation
: 적은 수의 데이터셋 있는 경우 시스템의 퍼포먼스 체크하는용으로 사용
단계)
- K개로 data set 나눔 (typically K = 5 or 10)
- K개의 덩어리 중 첫번째 것을 test set으로 두고, K-1개를 가지고 network train.
- 두번째 덩어리를 test set으로 두고 반복.
- 덩어리 바꾸며 train 하는 것을 K 회 반복. (train 할 때마다 W, b 업데이트)
- K test error(loss/cost) 평균 내서 estimated test error 얻음
Mismatched train/test distribution
: distribution이 같아야 한다.
검은 고양이 학습하면 test set의 흰 고양이 찾기 힘들꺼임 -> distribution이 다름
rule of thimb for splitting data:
- dev와 test set 같은 distribution
- test set 가지지 않는것 괜찮을 수 있다. (only dev set)
Bias and Variance
- bias와 variance는 tradeoff 관계.(하나 좋게 하면 하나 안좋아지는 관계)
-
최근에 deep learning era에서는 중요도 조금 줄었음
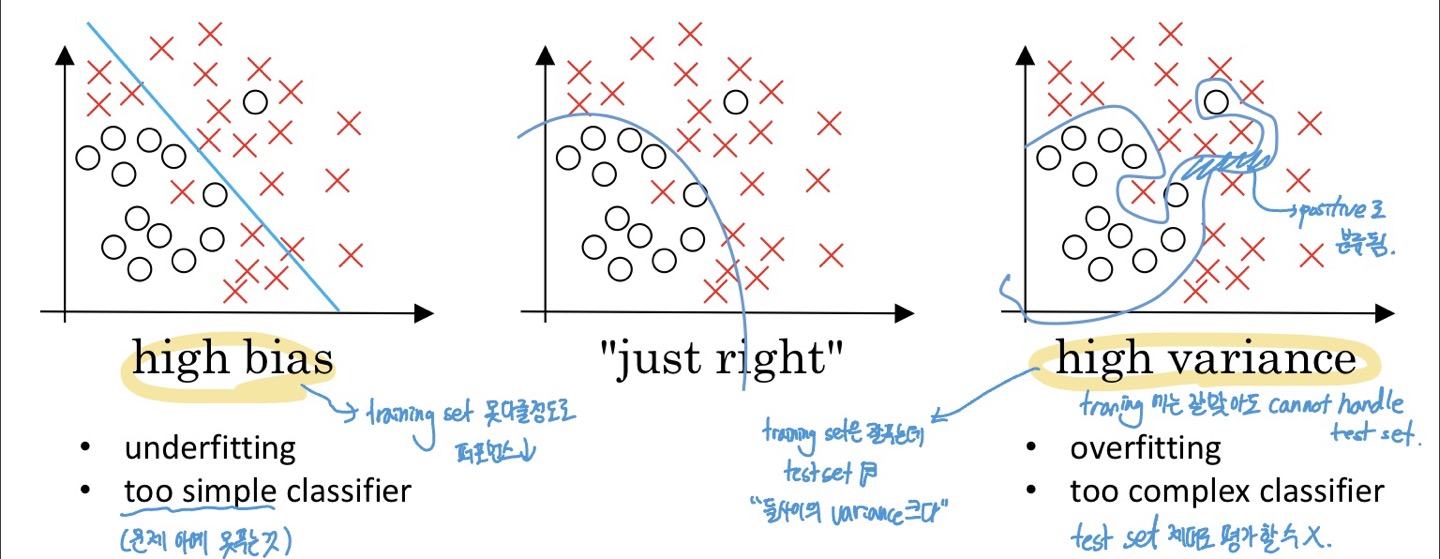
- High bias
- under fitting
- too simple classifier (문제 아예 못푸는 것)
- training set 못다룰 정도로 퍼포먼스 낮음
- High variance
- overfitting
- too complex classifier
- training에는 잘맞아도 test set handle 못함
- training set은 잘 푸는데 test set은 X = “둘 사이의 Variance 크다”
Q. 그래서 bias와 variance가 높은지는 어떻게 확인하나?
A.
Bias가 높은지 확인하고 싶으면 train set만 보면 된다. (train set error)
‘높다’는 것의 기준은 human error.
ex) 만약 human error가 0%에 가까우면, 15%는 높은것.
하지만 human error가 15%정도면, 15%는 high bias problem에 해당하지 않음.
Variance 확인하고 싶으면, train set과 dev set error의 차이를 보면 된다.
둘의 차이가 크면 high variance.
ex) train set error = 1% 인데, dev set error = 11% 인 경우
Basic recipe for machine learning
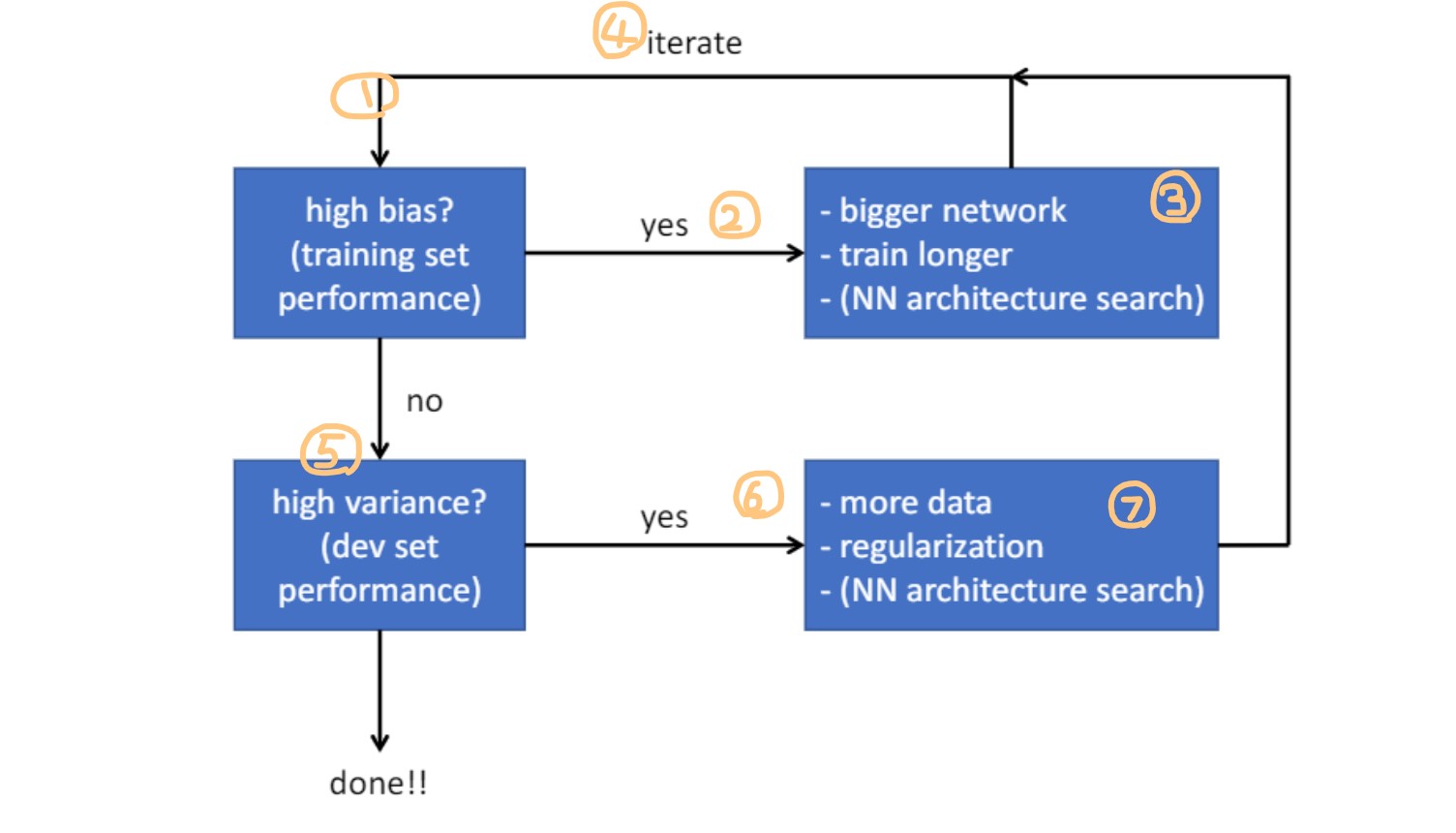
1 : 맨 먼저 bias 높은지 확인. (train set performance)
2 : 만약 높다면, high bias. 초등학생이 문제 푸는 상황
3 : 해결책은 고등학생으로 선수 바꾸는 것 = bigger network, 더 길게 학습 등
4 : 위 내용 반복해서 high bias 아니라면, 다음으로 넘어감
5 : high variance인지 확인. (dev set performance)
6 : 만약 높다면, 문제 외워서 푸는 상황(오버피팅)
7 : 해결책으로 문제 못외우게 많이 줘야지 = more data, regularizaation 등
High variance (overfitting) 해결책
- Regularization
- Dropout
- Data augmentation
- Early stopping
…
Regularization
- Weight가 너무 큰 값들을 가지지 않도록 하는 것
- Overfitting 막거나 Variance낮주는데 도움을 줌.
이렇게 모델의 Complexity와 데이터를 표현하는 정보의 규모가 서로 매칭되지 않을때 Underfit, Overfit이 일어나는 것을 Bad generalization이라고 논문에서 표현하고 있습니다.
데이터가 단순하고 모델이 복잡하면, 학습을 하면서 굉장히 작은 값이었던 weight들의 값이 점점 증가하게 되면서 Overfitting이 발생하게 됩니다. weight값이 커지게될 수록 학습데이터에 영향을 많이 받게 되고, 학습데이터에 딱 모델이 맞춰지게 되는 것이죠. 이를 ‘local noise의 영향을 크게 받아서, outlier들에 모델이 맞춰지는 현상’ 이라고 표현합니다.
\(J(w,b) = \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{i}, y^{i}) + \frac{\lambda}{2m} \vert \vert w \vert \vert^{2}_{2}\) 여기서 $\lambda$ : regularization parameter
L2 regularization: $\vert \vert w\vert \vert_{2}^{2} = \sum_{i=1}^{n} w_{j}^{2} = w^{T}w $
L1 regularization: $ \vert \vert w\vert \vert_{1} = \sum_{i=1}^{n}\vert m_{j}\vert $ -> (sparse w : 몇개의 큰 값 허용한다는 뜻)
(w 하단의 숫자가 1이면 L1 norm, 2면 ,L2 norm)
ex)
W = [W1,W2]
W1 = 0, W2 = 0.7 -> L2 = 0.49 L1 = 0.7
W1 = 0.4, W2 = 0.4 -> L2 = 0.32 L1 = 0.8
위 예시보면,
L2는 전반적으로 낮은 걸 선호하는 것을 볼 수 있고
L1은 엄청 큰게 하나 있어도 나며지가 0이면 좋다고 평가
따라서 퍼포먼스가 동일한 경우 위 두 경우 중
L2를 사용하면 밑의 경우를 선택할 것이고, L1을 사용하면 위의 경우를 선택.
위 original cost function으로 gradient계산하고 이를 통해 W 업데이트.
그리고 unknown W를 업데이트 할때 gradient만 사용하는 것이 아니라 페널티항을 더해서 가중치 축소.
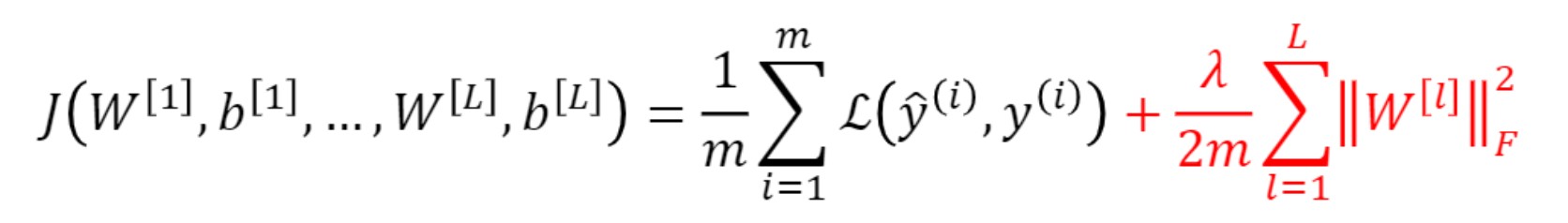

마지막 줄이 modified version.
L1, L2부분에서 물리적인 의미만 보면 W 작아지는것 선호하는걸 볼 수 있었음
동일한 이야기로
Gradient 계산까지 보면, 실제로 원래보다 W가 작아지는 것을 볼 수 있음
주의할 점) !!
regularization 너무 세게 걸면,
very large $\lambda$ -> $W^{[l]} \approx 0 $
대부분의 뉴런이 0이되고, high bias 문제 발생할 수 있음
작은 network로 high variance문제 해결할 수 있음
How does regularization prevent overfitting?
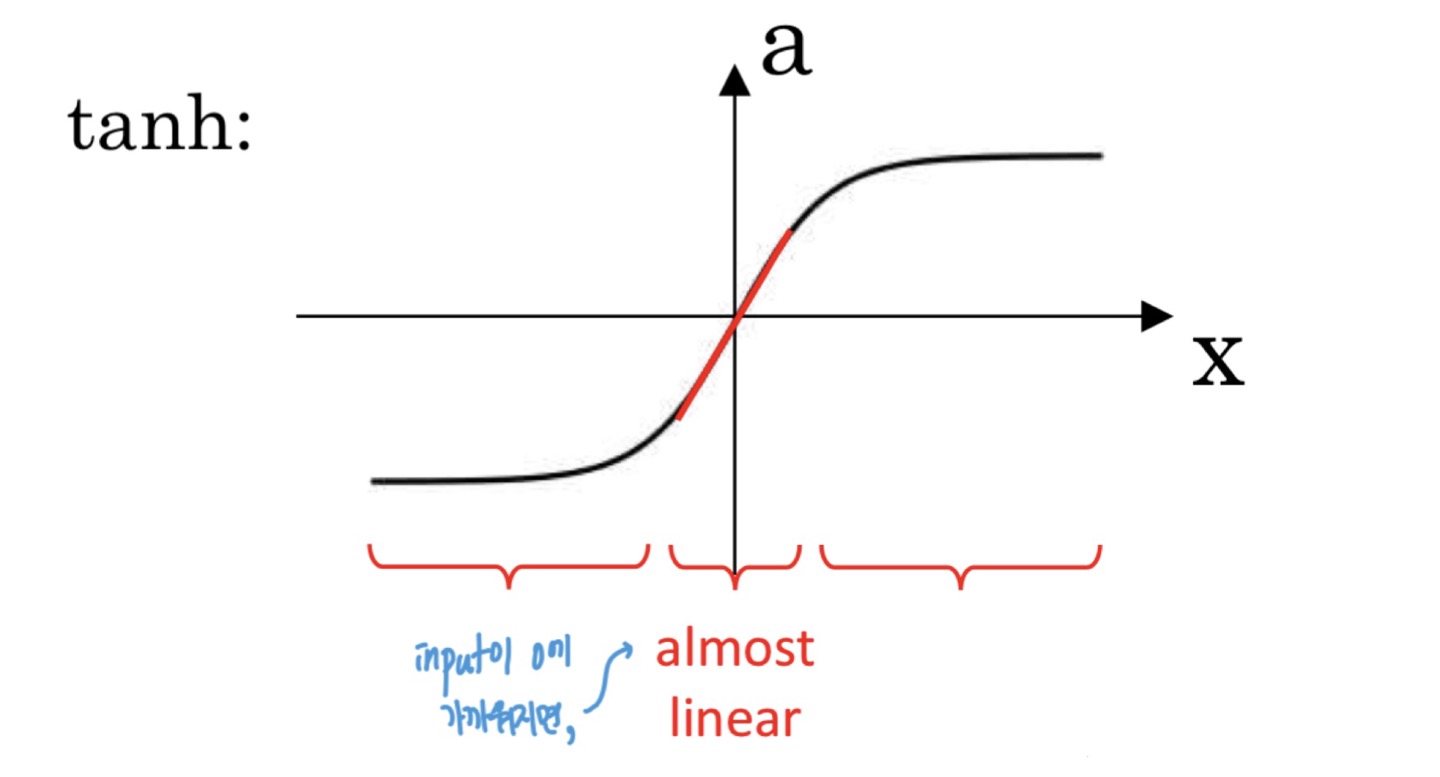
input이 0에 가까워지면, almost linear. 활성화 함수가 복잡도를 올리는 것을 완화시켜줌
디테일한 이유는 내 다른 포스트에서:
왜 활성화 함수 쓰는지
주의할 부분
뒤에 나오는 regularization은 input 값 자체를 정규화 하는것.
여기서는 z가 정규화 되는 대상.
Dropout regularization
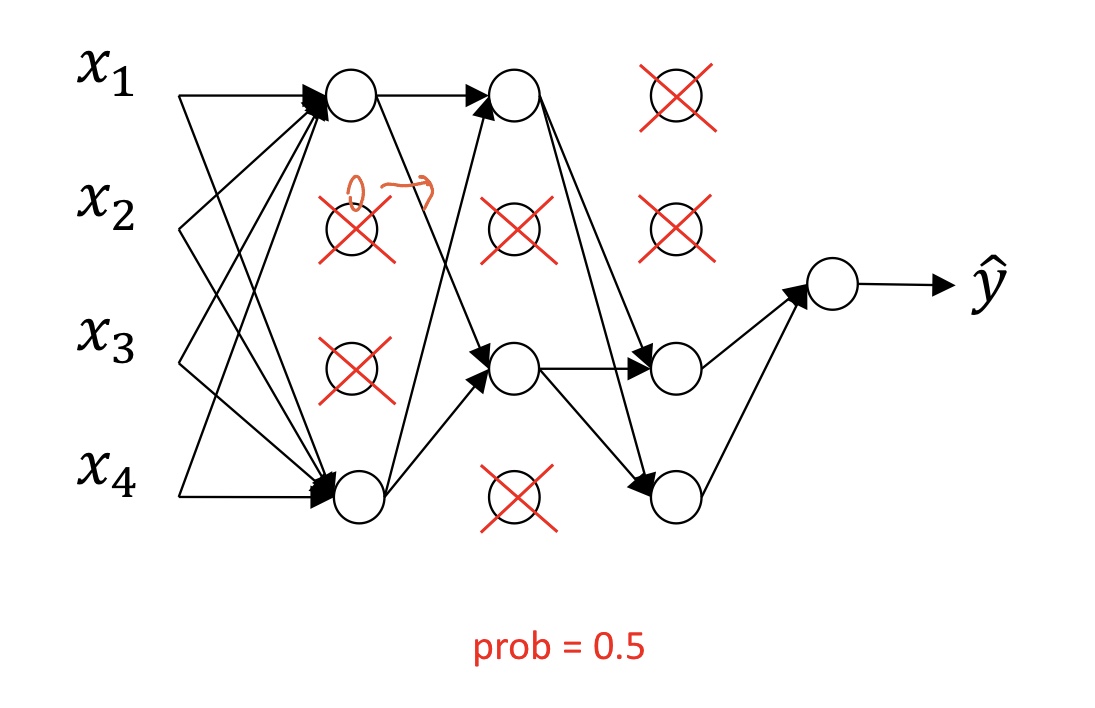
단계)
x표시된 것이 랜덤하게 제거됨
-> 네트워크는 simple, small하게 변함.
이후 다시 다른 뉴런들이 random하게 x표시 쳐짐
- training 단계에서만 unit remove함!
마지막 test시에는 다 사용 - x표시 한 노드의 output을 다음 layer에서 보지 못하게 하는 것.
- structure 자체를 다시 짜지않고. 구조는 동일하되, 값만.
- Intuition: Can’t rely on any one feature, thus spread out weights.
언제 없어질지 모르니 특정 노드에 중요한 일 맡길 수 X (W가 커질 수 X) - dropout의 확률은 hyper parameter.
- Layer 마다 다른 확률 쓸 수 O
하단 이미지는 dropout 구현하는 psudo code

“a3 /= keep_prob” 하는 이유:
Weight sum 될텐데, test 때 train 때와 비교해서 큰 값이 들어가지 않도록
이 부분은 test때에만 사용하는 부분.
$\because$ test 때에는 제거되는것 없이 전부 사용하기 때문에
Data augmentation
: over fitting 해결하는 다른 방법
이미지 flipping, rotating 등 geometry 변화.
마치 여러장의 그림 데이터가 있는 것 처럼 만들 수 O.
100% 효과있는 방법
Early stopping
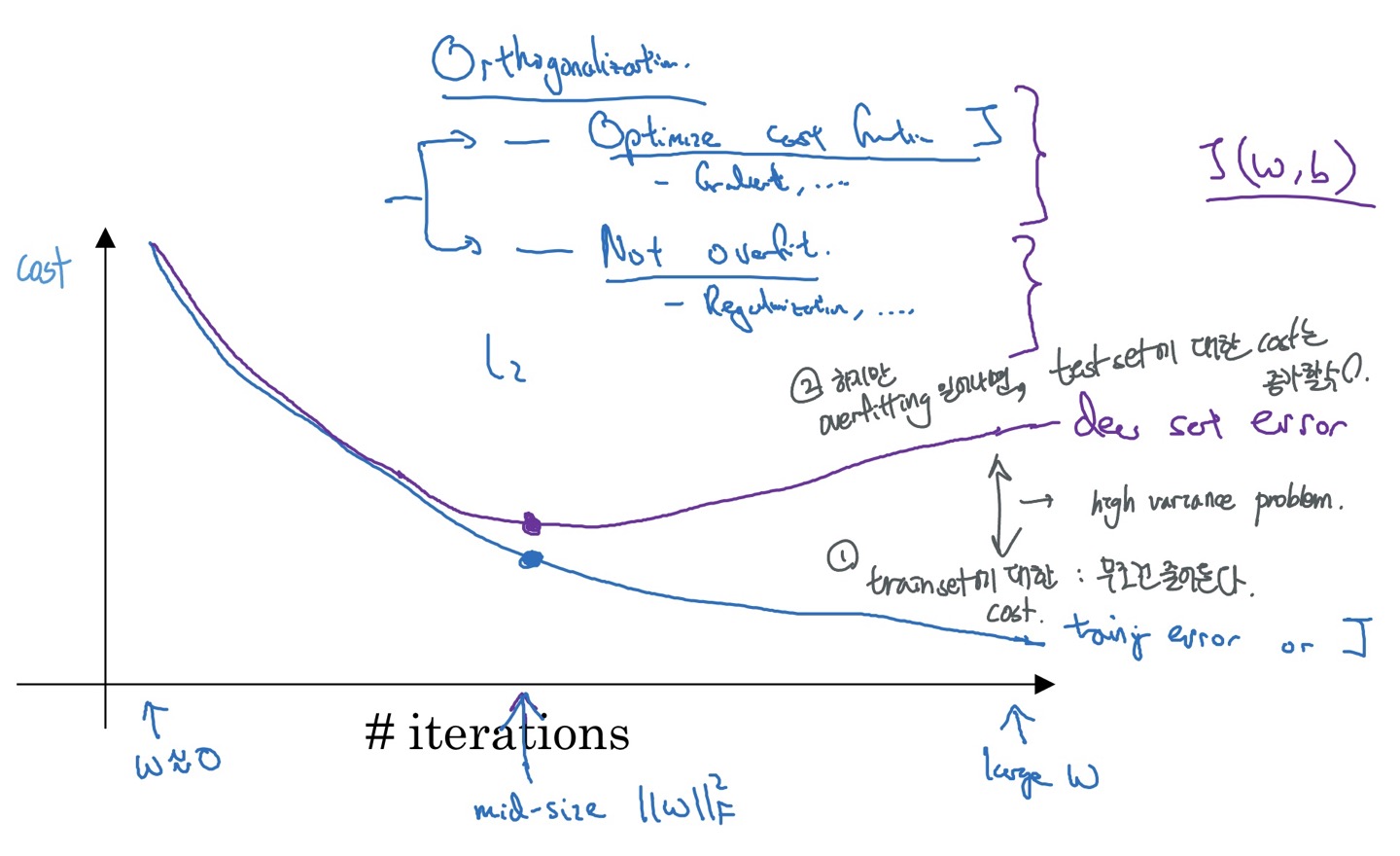
overfitting이 되었을 때 test set의 cost는 줄어들지만 train의 cost가 증가하는데, 이를 방지하기 위해 일찍 멈추는 것
Normalize training sets

단계)
Training set에서 mean 빼고,
normalize variance
=> zero mean, unit variance (평균 0, 분산1) 가지게도록 normalize 할 수 O
Why normalize inputs?
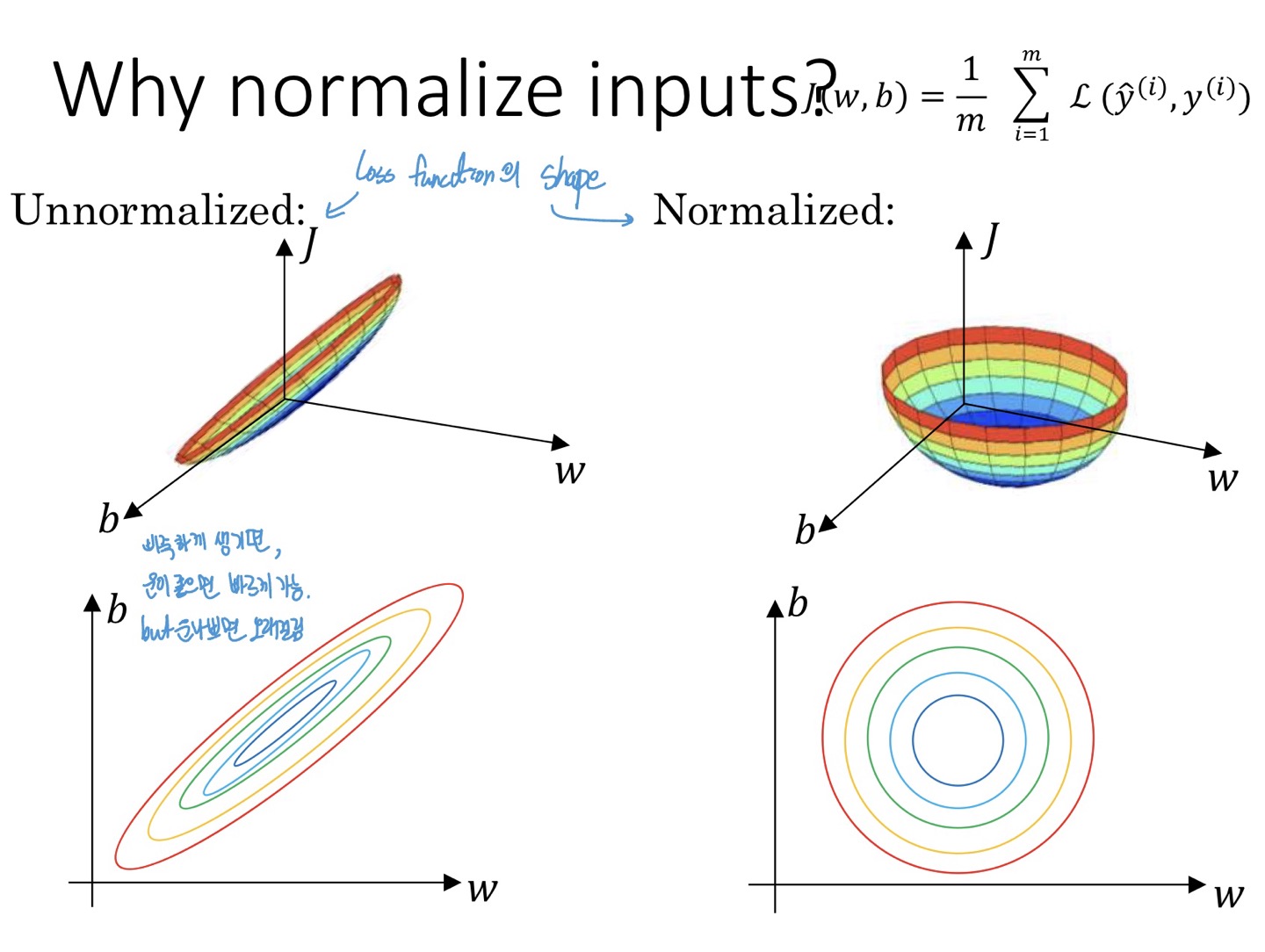
min 값 더 잘 찾아갈 수 있도록
Weight initialization for deep network
basic idea : large n -> smaller $W_{i}$
hidden layer 안에 hidden unit의 개수가 많아지면, W 작게 씀
Q. Output 결과가 너무 크지 않게 조절 위해 Weight initialization?
A. 경험적인 부분. 너무 크면 이상함 ex.1억
출처1 : 2023-1 ITE4052 수업
출처2 https://lsjsj92.tistory.com/391
출처3 https://simsim231.tistory.com/93
출처4 https://light-tree.tistory.com/125